已知向量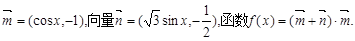
(Ⅰ)求f(x)的最小正周期T;
(Ⅱ)已知a,b,c分别为△ABC内角A,B,C的对边,A为锐角,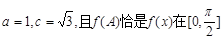 上的最大值,求A,b和△ABC的面积.
上的最大值,求A,b和△ABC的面积.
已知函数 在点
在点 处的切线与
处的切线与 轴平行。
轴平行。
(1)求实数 的值;
的值;
(2)证明: 。
。
(本小题满分12分)在平面直角坐标系 中,
中, 两点的坐标分别为
两点的坐标分别为 、
、 ,动点
,动点 满足:直线
满足:直线 与直线
与直线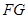 的斜率之积为
的斜率之积为 .
.
(1)求动点 的轨迹方程;
的轨迹方程;
(2)设 为动点
为动点 的轨迹的左右顶点,
的轨迹的左右顶点, 为直线
为直线 上的一动点(点
上的一动点(点 不在x轴上),连[
不在x轴上),连[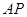 交
交 的轨迹于
的轨迹于 点,连
点,连 并延长交
并延长交 的轨迹于
的轨迹于 点,试问直线
点,试问直线 是否过定点?若成立,请求出该定点坐标,若不成立,请说明理由.
是否过定点?若成立,请求出该定点坐标,若不成立,请说明理由.
(本小题满分12分)如图,圆柱 内接直三棱柱
内接直三棱柱 ,该三棱柱的底面为圆柱底面的内接三角形,且
,该三棱柱的底面为圆柱底面的内接三角形,且 是圆
是圆 的直径,且
的直径,且 。在圆柱
。在圆柱 内随机选取一点,记该点取自于三棱柱
内随机选取一点,记该点取自于三棱柱 内的概率为
内的概率为

(1)当点 在圆周上运动时,求
在圆周上运动时,求 的最大值;
的最大值;
(2)记平面 与平面
与平面 所成的角为
所成的角为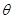
 ,当
,当 取最大值时,求
取最大值时,求 的值。
的值。
(本小题满分12分)在最近发生的飞机失联事件中,各国竭尽全力搜寻相关信息,为体现国际共产主义援助精神,中国海监某支队奉命搜寻某海域。若该海监支队共有 、
、 型两种海监船10艘,其中
型两种海监船10艘,其中 型船只7艘,
型船只7艘, 型船只3艘。
型船只3艘。
(1)现从中任选2艘海监船搜寻某该海域,求恰好有1艘 型海监船的概率;
型海监船的概率;
(2)假设每艘 型海监船的搜寻能力指数为5,每艘
型海监船的搜寻能力指数为5,每艘 型海监船的搜寻能力指数为10.现从这10艘海监船中随机的抽出4艘执行搜寻任务,设搜寻能力指数共为
型海监船的搜寻能力指数为10.现从这10艘海监船中随机的抽出4艘执行搜寻任务,设搜寻能力指数共为 ,求
,求 的分布列及期望.
的分布列及期望.
(本小题满分12分)在 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 .
.
(1)求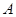 的大小;
的大小;
(2)若 ,求
,求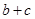 的取值范围.
的取值范围.