(本小题满分12分)在平面直角坐标系 中,
中, 两点的坐标分别为
两点的坐标分别为 、
、 ,动点
,动点 满足:直线
满足:直线 与直线
与直线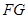 的斜率之积为
的斜率之积为 .
.
(1)求动点 的轨迹方程;
的轨迹方程;
(2)设 为动点
为动点 的轨迹的左右顶点,
的轨迹的左右顶点, 为直线
为直线 上的一动点(点
上的一动点(点 不在x轴上),连[
不在x轴上),连[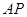 交
交 的轨迹于
的轨迹于 点,连
点,连 并延长交
并延长交 的轨迹于
的轨迹于 点,试问直线
点,试问直线 是否过定点?若成立,请求出该定点坐标,若不成立,请说明理由.
是否过定点?若成立,请求出该定点坐标,若不成立,请说明理由.
(1)下面的流程图表示了一个什么样的算法?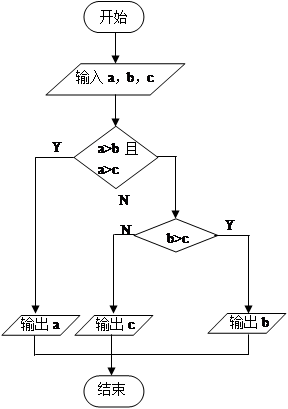
(2)思考:如果要实现上述流程图所表示的目的,是否还有其它的算法?
如果考生的成绩大于或等于60分,则输出“及格”,否则输出“不及格”,用流程图表示这一算法过程。
设计求解一元二次方程 的一个算法,并用流程图表示。
的一个算法,并用流程图表示。
任意给定三个正实数,设计一个算法,判断:以这样三个数为边长的三角形是否存在?画出它的框图。
星期天,刘先生到电信局打算上网开户,经询问,记录了可能需要的三种方式所花费的费用资料,现将资料整理如下:
1163普通:上网资费2元/小时;
2163A:每月50元(可上网50小时),超过50小时的部分资费2元/小时;
3ADSLD:每月70元,时长不限(其他因素忽略不计).
请你用所学的函数知识对上网方式与费用问题作出研究:
(1)分别写出三种上网方式中所用资费与时间的函数解析式;
(2)在同一坐标系内分别画出三种方式所需资费与时间的函数图象;
(3)根据你的研究,请给刘先生一个合理化的建议.