(本小题满分12分)
设 函数
函数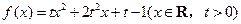 .
.
(Ⅰ)求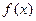 的最小值
的最小值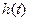 ;
;
(Ⅱ)若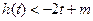 对
对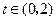 恒成立,求实数
恒成立,求实数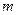 的取值范围.
的取值范围.
抛物线 上有两点
上有两点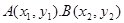 且
且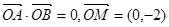 (0为坐标原点)
(0为坐标原点)
(1)求证: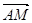 ∥
∥ (2)若
(2)若 ,求AB所在直线方程。
,求AB所在直线方程。
在△ABC中,a.b.c分别为内角A.B.C所对的边,且满足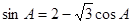
(1)求角A的大小
(2)现给出三个条件:①a=2.②B=45°③C= 试从中选出两个可以确定△ABC的条件写出你的
试从中选出两个可以确定△ABC的条件写出你的
选择,并以此为依据求△ABC的面积(只需写出一个选定方案即可,选多种方案以第一种方案记
分)
命题P:实数x满足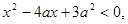 其中a<0,命题q:实数x满足
其中a<0,命题q:实数x满足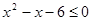 或
或 且
且 是
是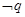 的必要不充分条件,求a的取值范围
的必要不充分条件,求a的取值范围
已知函数 的最大值是1,其图象经过点M
的最大值是1,其图象经过点M
(1)求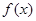 的解析式(2)已知
的解析式(2)已知 且
且 求
求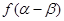 的值。
的值。
已知函数f(x)=lnx,g(x)= (a≠0)
(a≠0)
(1)若b=2,且h(x)=f(x)-g(x)在定义域上不单调,求a的取值范围;
(2)若a=1,b=-2设f(x)的图象C1与g(x)的图象C2交于点P、Q,过线段PQ的中点作x轴的垂线分别交C1,C2于点M、N,M、N的横坐标是m,求证:f'(m)<g'(m)。