(本小题满分12分)
已知中心在原点,焦点在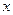 轴上的椭圆C的离心率为
轴上的椭圆C的离心率为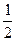 ,且经过点
,且经过点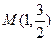 ,过点P(2,1)的直线
,过点P(2,1)的直线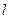 与椭圆C相交于不同的两点A、B.
与椭圆C相交于不同的两点A、B.
(Ⅰ)求椭圆C的方程;
(Ⅱ)是否存直线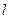 ,满足
,满足 ?
? 若存在,求出直线
若存在,求出直线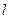 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
某公司向市场投放三种新型产品,经调查发现第一种产品受欢迎的概率为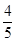 ,第二、第三种产品受欢迎的概率分别为
,第二、第三种产品受欢迎的概率分别为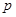 ,
, (
(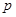 >
> ),且不同种产品是否受欢迎相互独立。记
),且不同种产品是否受欢迎相互独立。记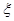 为公司向市场投放三种新型产品受欢迎的数量,其分布列为
为公司向市场投放三种新型产品受欢迎的数量,其分布列为
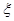 |
0 |
1 |
2 |
3 |
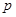 |
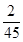 |
 |
 |
 |
(I)求该公司至少有一种产品受欢迎的概率;
(II)求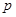 ,
, 的值;
的值;
(III)求数学期望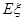 .
.
设函数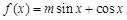
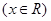 的图象经过点
的图象经过点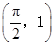 .
.
(I)求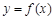 的解析式,并求函数的最小正周期和最值;
的解析式,并求函数的最小正周期和最值;
(II)若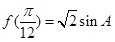 ,其中
,其中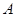 是面积为
是面积为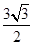 的锐角
的锐角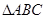 的内角,且
的内角,且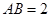 ,求边
,求边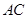 和
和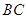 的长.
的长.
已知函数f(x)=ax-lnx(a为常数).
(Ⅰ)当a=1时,求函数f(x)的最小值;
(Ⅱ)求函数f(x)在[1,+∞)上的最值;
(Ⅲ)试证明对任意的n∈N﹡都有 <1.
<1.
如图,已知过点D(0,-2)作抛物线C1: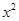 =2py(p>0)的切线l,切点A在第二象限.
=2py(p>0)的切线l,切点A在第二象限.
(Ⅰ)求点A的纵坐标;
(Ⅱ)若离心率为 的椭圆
的椭圆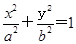 (a>b>0)恰好经过点A,设直线l交椭圆的另一点为B,记直线l,OA,OB的斜率分别为k,k1,k2,若k1+2k2=4k,求椭圆方程.
(a>b>0)恰好经过点A,设直线l交椭圆的另一点为B,记直线l,OA,OB的斜率分别为k,k1,k2,若k1+2k2=4k,求椭圆方程.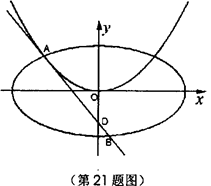
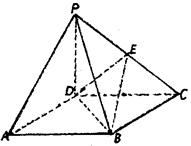
如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.
(Ⅰ)证明PA∥平面BDE;
(Ⅱ)求二面角B-DE-C的余弦值;
(Ⅲ)在棱PB上是否存在点F,使PB⊥平面DEF.证明你的结论.