如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点,
(I)求证:AC 1//平面CDB1;
(II)求二面角C1-AB-C的平面角的正切值。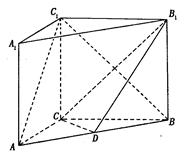
如图,已知四棱锥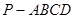 中,底面
中,底面 是直角梯形,
是直角梯形, ,
,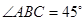 ,
,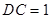 ,
, ,
, 平面
平面 ,
,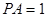 .
.
(Ⅰ)求证: 平面
平面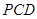 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)若 是
是 的中点,求三棱锥
的中点,求三棱锥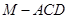 的体积.
的体积.
已知数列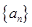 的前
的前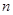 项和是
项和是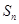 ,且
,且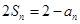 .
.
(Ⅰ)求数列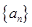 的通项公式;
的通项公式;
(Ⅱ)记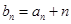 ,求数列
,求数列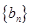 的前
的前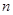 项和
项和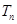
已知集合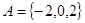 ,
,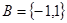 .
.
(Ⅰ)若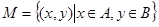 ,用列举法表示集合
,用列举法表示集合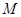 ;
;
(Ⅱ)在(Ⅰ)中的集合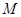 内,随机取出一个元素
内,随机取出一个元素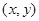 ,求以
,求以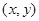 为坐标的点位于区域D:
为坐标的点位于区域D: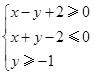 内的概率.
内的概率.
设函数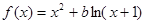 ,其中
,其中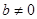 .(Ⅰ)若
.(Ⅰ)若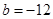 ,求
,求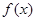 在
在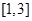 上的最小值;
上的最小值;
(Ⅱ)如果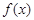 在定义域内既有极大值又有极小值,求实数
在定义域内既有极大值又有极小值,求实数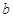 的取值范围;
的取值范围;
(Ⅲ)是否存在最小的正整数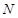 ,使得当
,使得当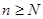 时,不等式
时,不等式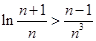 恒成立.
恒成立.
椭圆 的离心率为
的离心率为 ,右焦点到直线
,右焦点到直线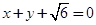 的距离为
的距离为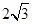 ,过
,过 的直线
的直线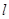 交椭圆于
交椭圆于 两点
两点 .
.
(Ⅰ) 求椭圆的方程;
(Ⅱ) 若直线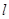 交
交 轴于
轴于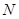 ,
, ,求直线
,求直线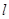 的方程
的方程 .
.