(本小题满分12分)
已知 是奇函数
是奇函数
(Ⅰ)求 的值,并求该函数的定义域;
的值,并求该函数的定义域;
(Ⅱ)根据(Ⅰ)的结果,判 断
断 在
在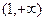 上的单调性,并给出证明.
上的单调性,并给出证明.
设实数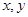 满足不等式组
满足不等式组 。
。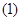 作出点
作出点 所在的平面区域并求出
所在的平面区域并求出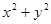 的取值范围;
的取值范围; 设
设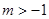 ,在
,在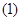 所求的区域内,求
所求的区域内,求 的最值。
的最值。
已知函数 ,输入自变量的值,输出对应的函数值。
,输入自变量的值,输出对应的函数值。
(1)画出算法框图;
(2)写出程序语句。
某车间为了规定工时定额,需要确定加个某零件所花费的时间,为此作了四次实验,得到的数据如下:
| 零件的个数x(个) |
2 |
3 |
4 |
5 |
| 加工的时间y(小时) |
2.5 |
3 |
4 |
4.5 |
(1)求出y关于x的线性回归方程;
(2)试预测加工10个零件需要多少时间?
已知实数x、y满足
(1)求不等式组表示的平面区域的面积;
(2)若目标函数为z=x-2y,求z的最小值.
对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
| 甲 |
27 |
38 |
30 |
37 |
35 |
31 |
| 乙 |
33 |
29 |
38 |
34 |
28 |
36 |
(1)画出茎叶图,由茎叶图判断哪位选手的成绩较稳定?
(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、中位数、标准差,并判断选谁参加比赛更合适.