某公司在过去几年内使用某种型号的灯管1000支,该公司对这些灯管的使用寿命
(单位:小时)进行了统计,统计结果如下表所示:
| 分组 |
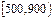 |
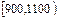 |
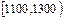 |
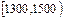 |
 |
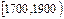 |
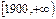 |
| 组数 |
48 |
121 |
208 |
223 |
193 |
165 |
42 |
| 频率 |
|
|
|
|
|
|
|
(1)将各组的频率填入表中;
(2)根据上述统计结果,计算灯管使用寿命不足1500小时的频率;
(3)该公司某办公室新安装了这种型号的灯管3支,若将上述频率作为概率,试求至少有2支灯管的使用寿命不足1500小时的概率
(本小题满分12分)如图,直角梯形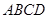 与等腰直角三角形
与等腰直角三角形 所在的平面互相垂直.
所在的平面互相垂直. ∥
∥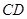 ,
,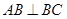 ,
, ,
,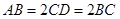 .
.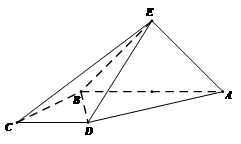
(Ⅰ)求证: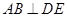 ;
;
(Ⅱ)求二面角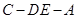 余弦值.
余弦值.
(本小题满分12分)某工厂生产甲、乙两种芯片,其质量按测试指标划分为:指标大于或等于82为合格品,小于82为次品.现随机抽取这两种芯片各100件进行检测,检测结果统计如下:
(Ⅰ)试分别估计芯片甲,芯片乙为合格品的概率;
(Ⅱ)生产一件芯片甲,若是合格品可盈利40元,若是次品则亏损5元;生产一件芯片乙,若是合格品可盈利50元,若是次品则亏损10元.在(Ⅰ)的前提下,记X为生产1件芯片甲和1件芯片乙所得的总利润,求随机变量X的概率分布列和数学期望值.
(本小题满分12分)已知 是公差为2的等差数列,且
是公差为2的等差数列,且 是
是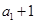 与
与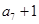 的等比中项.
的等比中项.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)令 ,求数列
,求数列 的前
的前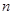 项和
项和 .
.
(本小题满分10分)选修4—5:不等式选讲
设函数 .
.
(Ⅰ)解不等式: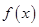 >0;
>0;
(Ⅱ)若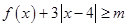 对一切实数χ均成立,求m的取值范围.
对一切实数χ均成立,求m的取值范围.
(本小题满分10分)选修4—4:坐标系与参数方程
已知曲线C的极坐标方程是ρ=4cosθ,以极点为平面直角坐标系的原点,极轴为χ轴的正半轴,建立平
面直角坐标系,直线l的参数方程是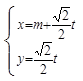 (t是参数).
(t是参数).
(Ⅰ)将曲线C的极坐标方程化为直角坐标方程,直线l的参数方程化为普通方程;
(Ⅱ)若直线l与曲线C相交于A、B两点,且|AB|= ,试求实数m的值.
,试求实数m的值.