某种产品的广告费用支出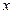万元与销售额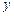万元之间有如下的对应数据：-优题课

某种产品的广告费用支出万元与销售额万元之间有如下的对应数据：

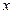	2	4	5	6	8
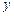	20	30	50	50	70

（1）画出上表数据的散点图；
（2）根据上表提供的数据，求出y关于x的线性回归方程；
（3）据此估计广告费用为10万元时，所得的销售收入．
(参考数值：，，)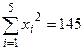

科目数学题型解答题难度较易

设抛物线 $C : x^{2} = 2 p y (p > 0)$ 的焦点为 $F$ ,准线为 $l$ , $A \in C$ ,已知以 $F$ 为圆心, $F A$ 为半径的圆 $F$ 交 $l$ 于 $B, D$ 两点；
（1）若 $∠ B F D = 90^{°}$ , $∆ A B D$ 的面积为 $4 \sqrt{2}$ ；求 $p$ 的值及圆 $F$ 的方程；
（2）若 $A, B, F$ 三点在同一直线 $m$ 上，直线 $n$ 与 $m$ 平行，且 $n$ 与 $C$ 只有一个公共点,求坐标原点到 $m, n$ 距离的比值.

如图，直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A C = B C = \frac{1}{2} A A_{1}$ ， $D$ 是棱 $A A_{1}$ 的中点， $D C_{1} ⊥ B D$ .

（1）证明： $D C_{1} ⊥ B C$

（2）求二面角 $A_{1} - B D - C_{1}$ 的大小.

某花店每天以每枝 $5$ 元的价格从农场购进若干枝玫瑰花，然后以每枝 $10$ 元的价格出售，如果当天卖不完，剩下的玫瑰花作垃圾处理.
（1）若花店一天购进 $16$ 枝玫瑰花，求当天的利润 $y$ (单位：元)关于当天需求量 $n$ （单位：枝， $n \in N$ ）的函数解析式.
（2）花店记录了100天玫瑰花的日需求量（单位：枝），整理得下表：

以100天记录的各需求量的频率作为各需求量发生的概率.
（i）若花店一天购进 $16$ 枝玫瑰花， $X$ 表示当天的利润（单位：元），求 $X$ 的分布列，数学期望及方差；
（ii）若花店计划一天购进16枝或17枝玫瑰花，你认为应购进16枝还是17枝？请说明理由.

已知 $a, b, c$ 分别为 $∆ A B C$ 三个内角 $A, B, C$ 的对边, $a \cos C + \sqrt{3} a \sin C - b - c = 0$

（1）求 $A$

（2）若 $a = 2$ , $∆ A B C$ 的面积为 $\sqrt{3}$ ,求 $b, c$ .

数列 $\{x_{n}\}$ 满足： $x_{1} = 0, x_{n + 1} = - {x_{n}}^{2} + x_{n} + c (n \in N^{+})$

（I）证明：数列 $\{x_{n}\}$ 是单调递减数列的充分必要条件是 $c < 0$

（II）求 $c$ 的取值范围，使数列 $\{x_{n}\}$ 是单调递增数列。

试卷网试题网古诗词网作文网范文网