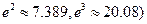设抛物线
的焦点为
,准线为
,
,已知以
为圆心,
为半径的圆
交
于
两点;
(1)若
,
的面积为
;求
的值及圆
的方程;
(2)若
三点在同一直线
上,直线
与
平行,且
与
只有一个公共点,求坐标原点到
距离的比值.
(本题满分16分,第(1)小题6分,第(2)小题10分)
某团体计划于2011年年初划拨一笔款项用于设立一项基金,这笔基金由投资公司运作,每年可有3%的受益.
(1)该笔资金中的A(万元)要作为保障资金,每年年末将本金A及A的当年受益一并作为来年的投资继续运作,直到2020年年末达到250(万元),求A的值;
(2)该笔资金中的B(万元)作为奖励资金,每年年末要从本金B及B的当年受益中支取250(万元),余额来年继续运作,并计划在2020年年末支取后该部分资金余额为0,求B的值.(A和B的结果以万元为单位,精确到万元)
(本题满分14分,第(1)小题6分,第(2)小题8分)
四棱锥P-ABCD中,PD⊥平面ABCD,PA与平面ABCD所成的角为60 ,在四边形ABCD中,∠ADC=∠DAB=90
,在四边形ABCD中,∠ADC=∠DAB=90 ,AB=4,CD=1,AD=2.
,AB=4,CD=1,AD=2.
(1)求四棱锥P-ABCD的体积;
(2)求异面直线PA与BC所成的角.
(本题满分12分,第(1)小题5分,第(2)小题7分)
已知锐角△ABC中,三个内角为A、B、C,向量 =
= 2-2
2-2 ,
, +
+
 ,
, =
=
 -
- ,1+
,1+
 ,
, ∥
∥ .
.
(1)求∠A的大小;
(2)求函数 =2
=2 +
+ 取得最大值时,∠B的大小.
取得最大值时,∠B的大小.
已知椭圆的中心在原点,焦点在x轴上,离心率为 ,过点
,过点 与椭圆交于
与椭圆交于 两点.
两点.
(1)若直线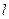 的斜率为1,且
的斜率为1,且 ,求椭圆的标准方程;
,求椭圆的标准方程;
(2)若(1)中椭圆的右顶点为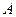 ,直线
,直线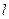 的倾斜角为
的倾斜角为 ,问
,问 为何值时,
为何值时, 取得最大值,并求出这个最大值.
取得最大值,并求出这个最大值.
设函数

(1)若 ,
,
①求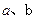 的值;
的值;
②在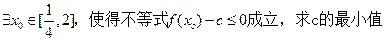 ;
;
(2)当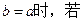
 上是单调函数,求
上是单调函数,求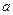 的取值范围。
的取值范围。
(参考数据