设函数

(1)若 ,
,
①求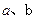 的值;
的值;
②在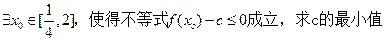 ;
;
(2)当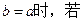
 上是单调函数,求
上是单调函数,求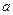 的取值范围。
的取值范围。
(参考数据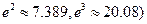
(本小题满分12分)
某地区对12岁儿童瞬时记忆能力进行调查.瞬时记忆能力包括听觉记忆能力与视觉记忆能力.某班学生共有40人,下表为该班学生瞬时记忆能力的调查结果.例如表中听觉记忆能力为中等,且视觉记忆能力偏高的学生为3人.
 视觉 视觉 |
视觉记忆能力 |
||||
| 偏低 |
中等 |
偏高 |
超常 |
||
| 听觉 记忆 能力 |
偏低 |
0 |
7 |
5 |
1 |
| 中等 |
1 |
8 |
3 |
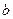 |
|
| 偏高 |
2 |
 |
0 |
1 |
|
| 超常 |
0 |
2 |
1 |
1 |
由于部分数据丢失,只知道从这40位学生中随机抽取一个,视觉记忆能力恰为中等,且听觉记忆能力为中等或中等以上的概率为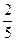 .
.
(1)试确定 、
、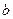 的值;
的值;
(2)从40人中任意抽取1人,求此人听觉记忆能力恰为中等,且视觉记忆能力为中等或中等以上的概率.
平面直角坐标系中,将曲线 (
( 为参数)上的每一点纵坐标不变,横坐标变为原来的一半,然后整个图象向右平移
为参数)上的每一点纵坐标不变,横坐标变为原来的一半,然后整个图象向右平移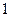 个单位,最后横坐标不变,纵坐标变为原来的2倍得到曲线
个单位,最后横坐标不变,纵坐标变为原来的2倍得到曲线 .以坐标原点为极点,
.以坐标原点为极点, 的非负半轴为极轴,建立的极坐标中的曲线
的非负半轴为极轴,建立的极坐标中的曲线 的方程为
的方程为 ,求
,求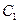 和
和 公共弦的长度.
公共弦的长度.
(本小题满分10分)选修4-1:几何证明选讲
如图,直线AB过圆心O,交圆O于A、B,直线AF交圆O于F(不与B重合),直线 与圆O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.
与圆O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.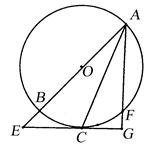
求证:(Ⅰ)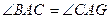 ;
;
(Ⅱ) .
.
已知函数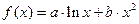 在点
在点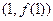 处的切线方程为
处的切线方程为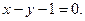
(Ⅰ)求 的表达式;
的表达式;
(Ⅱ)若 满足
满足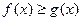 恒成立,则称
恒成立,则称 的一个“上界函数”,如果
的一个“上界函数”,如果
函数 为
为 (
(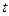 为实数)的一个“上界函数”,求
为实数)的一个“上界函数”,求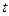 的取值范围;
的取值范围;
(Ⅲ)当 时,讨论
时,讨论 在区间(0,2)上极值点的个数.
在区间(0,2)上极值点的个数.
已知椭圆方程为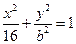
 ,P为椭圆上的动点,F1、F2为椭圆的两焦点,当点P不在x轴上时,过F1作∠F1PF2的外角平分线的垂线F1M,垂足为M,当点P在x轴上时,定义M与P重合.
,P为椭圆上的动点,F1、F2为椭圆的两焦点,当点P不在x轴上时,过F1作∠F1PF2的外角平分线的垂线F1M,垂足为M,当点P在x轴上时,定义M与P重合.
(Ⅰ)求M点的轨迹T的方程;
(Ⅱ)已知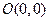 、
、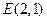 ,试探究是否存在这样的点
,试探究是否存在这样的点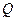 :
: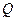 是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积
是轨迹T内部的整点(平面内横、纵坐标均为整数的点称为整点),且△OEQ的面积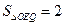 ?若存在,求出点Q的坐标,若不存在,说明理由.
?若存在,求出点Q的坐标,若不存在,说明理由.