如图所示,在▱ABCD中,已知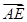 =
=
 ,
,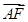 =
=
 .
.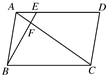
求证:B、F、E三点共线.
已知△ABC中,A(7,8),B(3,5),C(4,3),M、N是AB、AC的中点,D是BC的中点,MN与AD交于点F,求 .
.
已知正三棱锥S-ABC的底面边长为a,高为h,在正三棱锥内取一点M,试求点M到底面的距离小于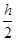 的概率.
的概率.
街道旁边有一游戏:在铺满边长为9 cm的正方形塑料板的宽广地面上,掷一枚半径为1 cm的小圆板,规则如下:每掷一次交5角钱,若小圆板压在边上,可免费重掷一次;若小圆板全部落在正方形内可再交5角,再掷一次;若小圆板压在塑料板的顶点上,可获得一元钱.试问:
(1)小圆板压在塑料板的边上的概率是多少?
(2)小圆板压在塑料板顶点上的概率是多少?
平面上画了两条平行且相距2a的平行线.把一枚半径r<a的硬币任意投掷在这个平面上,求硬币不与任一条平行线相碰的概率.