(本小题满分12分)
如图，在四棱锥P－ABCD中，PA
底面ABCD,
DAB为直角，AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点．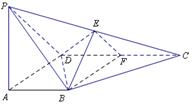
（Ⅰ）试证：AB平面BEF；
（Ⅱ）设PA＝k·AB，若平面
与平面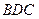
的夹角大于
，求k的取值范围．
为了解心肺疾病是否与年龄相关，现随机抽取了40名市民，得到数据如下表：
| 患心肺疾病 |
不患心肺疾病 |
合计 |
|
| 大于40岁 |
16 |
||
| 小于等于40岁 |
12 |
||
| 合计 |
40 |
已知在全部的40人中随机抽取1人，抽到不患心肺疾病的概率为
（1）请将
列联表补充完整；
（2）已知大于40岁患心肺疾病市民中，经检查其中有4名重症患者，专家建议重症患者住院治疗，现从这16名患者中选出两名，记需住院治疗的人数为
，求的分布列和数学期望；
（3）能否在犯错误的概率不超过0.01的前提下认为患心肺疾病与年龄有关？
下面的临界值表供参考：
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
（参考公式：
，其中
）
若数列
的前
项和
满足
,等差数列
满足
.
(1)求数列、的通项公式;
(2)设
,求数列
的前项和为
.
已知直角梯形
,
，
，
沿
折叠成三棱锥，当三棱锥体积最大时，求此时三棱锥外接球的体积
某市为了解社区群众体育活动的开展情况，拟采用分层抽样的方法从A,B,C三个行政区抽出6个社区进行调查.已知A，B，C行政区中分别有12，18，6个社区.
（1）求从A,B,C三个行政区中分别抽取的社区个数；
（2）若从抽得的6个社区中随机的抽取2个进行调查结果的对比，求抽取的2个社区中至少有一个来自A行政区的概率.
已知函数
.
（1）求函数
的最小正周期；
（2）在
中，若
的值.