( (本小题满分12分)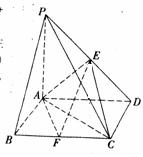
在四棱锥P-ABCD中,底面ABCD是矩形,PA=AD=4,AB=2,
PB=2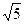 ,PD
,PD =4
=4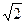 ,E是PD的中点
,E是PD的中点
(1)求证:AE⊥平面PCD;
(2)若F是线段BC的中点,求三棱锥F-ACE的体积。
在如图所示的空间几何体中,平面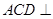 平面ABC,
平面ABC,
AB=BC=CA=DA=DC=BE=2,BE和平面ABC所成的角为60°,且点E在平面ABC上的射影落在 的平分线上。
的平分线上。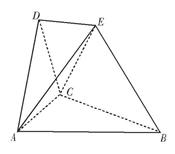
(1)求证:DE//平面ABC;
(2)求二面角E—BC—A的余弦值;
一个盒子中装有5张卡片,每张卡片上写有一个数字,数字分别是1、2、3、4、5,现从盒子中随机抽取卡片。
(1)从盒中依次抽取两次卡片,每次抽取一张,取出的卡片不放回,求两次取到的卡片的数字既不全是奇数,也不全是偶数的概率;
(2)若从盒子中有放回的抽取3次卡片,每次抽取一张,求恰有两次取到卡片的数字为偶数的概率;
(3)从盒子中依次抽取卡片,每次抽取一张,取出的卡片不放回,当放回记有奇数的卡片即停止抽取,否则继续抽取卡片,求抽取次数X的分布列和期望。
已知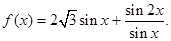
(1)求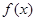 的最大值,及当取最大值时x的取值集合。
的最大值,及当取最大值时x的取值集合。
(2)在三角形ABC中,a,b,c分别是角A,B,C所对的边,对定义域内任意x,有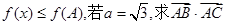 的最大值.
的最大值.
(本小题满分14分)已知函数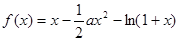 ,其中
,其中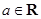 .
.
(Ⅰ)若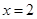 是
是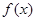 的极值点,求
的极值点,求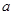 的值;
的值;
(Ⅱ)求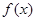 的单调区间;
的单调区间;
(Ⅲ)若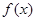 在
在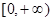 上的最大值是
上的最大值是 ,求
,求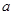 的取值范围)
的取值范围)
已知椭圆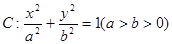 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴为半径的圆与直线
,以原点为圆心,椭圆的短半轴为半径的圆与直线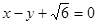 相切.
相切.
(I)求椭圆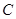 的方程;
的方程;
(II)设P(4,0),A,B是椭圆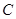 上关于
上关于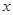 轴对称的任意两个不同的点,连接
轴对称的任意两个不同的点,连接 交椭圆
交椭圆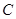 于另一点
于另一点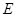 ,证明直线
,证明直线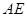 与
与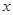 轴相交于定点
轴相交于定点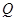 ;
;
(Ⅲ)在(II)的条件下,过点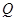 的直线与椭圆
的直线与椭圆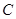 交于
交于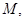
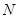 两点,求
两点,求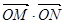 的取值范围.
的取值范围.