已知曲线 与
与 在第一象限内的交点为P.
在第一象限内的交点为P.
(1)求过点 且与曲线
且与曲线 相切的直线方程
相切的直线方程 ;
;
(2)求 与曲线
与曲线 所围图形的面积
所围图形的面积 .
.
已知函数 处都取得极值.
处都取得极值.
(1)求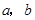 的值;
的值;
(2)求 的单调区间
的单调区间
已知 在
在 上是单调增函数,则
上是单调增函数,则 的最大值是( )
的最大值是( )
| A.0 | B.1 | C.3 | D.12 |
已知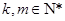 ,若存在互不相等的正整数
,若存在互不相等的正整数 …
…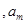 ,使得
,使得 …
… 同时小于
同时小于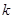 ,则记
,则记 为满足条件的
为满足条件的 的最大值.
的最大值.
(1)求 的值;
的值;
(2)对于给定的正整数
 ,
,
(ⅰ)当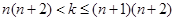 时,求
时,求 的解析式;
的解析式;
(ⅱ)当 时,求
时,求 的解析式.
的解析式.
如图,在直三棱柱ABC—A1B1C1中,AC = 3,BC = 4,AB = 5,AA1 = 4.
(1)设 ,异面直线AC1与CD所成角的余弦值为
,异面直线AC1与CD所成角的余弦值为 ,求
,求 的值;
的值;
(2)若点D是AB的中点,求二面角D—CB1—B的余弦值.