如图,在直三棱柱ABC—A1B1C1中,AC = 3,BC = 4,AB = 5,AA1 = 4.
(1)设 ,异面直线AC1与CD所成角的余弦值为
,异面直线AC1与CD所成角的余弦值为 ,求
,求 的值;
的值;
(2)若点D是AB的中点,求二面角D—CB1—B的余弦值.
在平面直角坐标系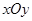 中,点
中,点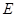 到两点
到两点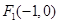 ,
, 的距离之和为
的距离之和为 ,设点
,设点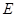 的轨迹为曲线
的轨迹为曲线 .
.
(1)写出 的方程;
的方程;
(2)设过点 的斜率为
的斜率为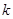 (
( )的直线
)的直线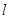 与曲线
与曲线 交于不同的两点
交于不同的两点 ,
,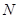 ,点
,点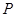 在
在 轴上,且
轴上,且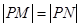 ,求点
,求点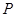 纵坐标的取值范围.
纵坐标的取值范围.
在直三棱柱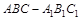 中,
中,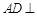 平面
平面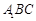 ,其垂足
,其垂足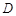 落在直线
落在直线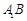 上.
上.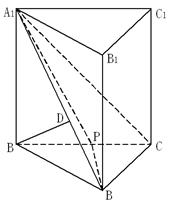
(1)求证: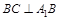 ;
;
(2)若 ,
,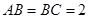 ,
,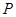 为
为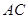 的中点,求三棱锥
的中点,求三棱锥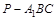 的体积.
的体积.
某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查,以计算每户每月的碳排放量.若月排放量符合低碳标准的称为“低碳族”,否则称为“非低碳族”.若小区内有至少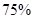 的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区”.已知备选的5个居民小区中有三个非低碳小区,两个低碳小区.
的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区”.已知备选的5个居民小区中有三个非低碳小区,两个低碳小区.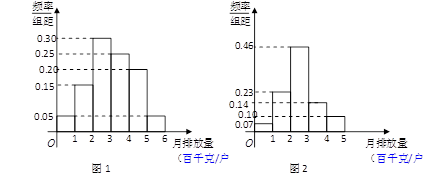
(1)求所选的两个小区恰有一个为“非低碳小区”的概率;
(2)假定选择的“非低碳小区”为小区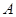 ,调查显示其“低碳族”的比例为
,调查显示其“低碳族”的比例为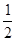 ,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区
,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区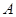 是否达到“低碳小区”的标准?
是否达到“低碳小区”的标准?
已知等差数列 的公差
的公差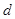 大于0,且
大于0,且 是方程
是方程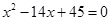 的两根,数列
的两根,数列 的前
的前 项和为
项和为 ,
,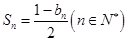 .
.
(1)求数列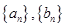 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 .
.
已知函数f(x)=x2+ (x≠0).
(x≠0).
(1)判断f(x)的奇偶性,并说明理由;
(2)若f(1)=2,试判断f(x)在[2,+∞)上的单调性