(本小题14分)
在平面直角坐标系xoy中,给定三点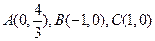 ,点P到直线BC的距离是该点到直线AB,AC距离的等比中项。
,点P到直线BC的距离是该点到直线AB,AC距离的等比中项。
(Ⅰ)求点P的轨迹方程;
(Ⅱ)若直线L经过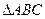 的内心(设为D),且与P点的轨迹恰好有3个公共点,求L的斜率k的取值范围。
的内心(设为D),且与P点的轨迹恰好有3个公共点,求L的斜率k的取值范围。
(本小题满分l4分)已知数列 的前n项和为
的前n项和为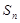 ,正数数列
,正数数列 中
中
(e为自然对数的底 )且
)且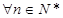 总有
总有 是
是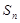 与
与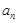 的等差中项,
的等差中项,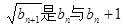 的等比中项.
的等比中项.
(1) 求证: 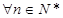 有
有 ;
;
(2) 求证: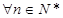 有
有 .
.
(本小题满分l4分)如图,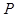 是抛物线
是抛物线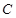 :
: 上横坐标大于零的一点,直线
上横坐标大于零的一点,直线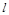 过点
过点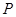 并与抛物线
并与抛物线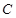 在点
在点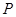 处的切线垂直,直线
处的切线垂直,直线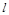 与抛物线
与抛物线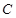 相交于另一点
相交于另一点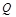 .
.
(1)当点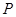 的横坐标为2时,求直线
的横坐标为2时,求直线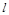 的方程;
的方程;
(2)若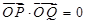 ,求过点
,求过点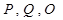 的圆的方程.
的圆的方程.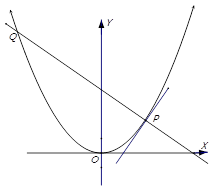
(本小题满分14分)已知函数 .
.
(1)设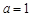 时,求函数
时,求函数 极大值和极小值;
极大值和极小值;
(2) 时讨论函数
时讨论函数 的单调区间.
的单调区间.
(本小题满分14分)
如图,四边形 中(图1),
中(图1), 是
是 的中点,
的中点, ,
,
 ,
, 将(图1)沿直线
将(图1)沿直线 折起,使二面角
折起,使二面角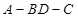 为
为 (如图2)
(如图2)
(1)求证: 平面
平面 ;
;
(2)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(3)求点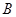 到平面
到平面 的距离.
的距离.
(本小题满分12分)
甲、乙两人各射击一次,击中目标的概率分别是 和
和 假设两人射击是否击中目标,相互
假设两人射击是否击中目标,相互
之间没有影响;每人各次射击是否击中目标,相互之间也没有影响
(1)甲射击3次,至少1次未击中目标的概率;
(2)假设某人连续2次未击中目标,则停止射击,问:乙恰好射击4次后,被中止射击的概率是多少?
⑶设甲连续射击3次,用 表示甲击中目标时射击的次数,求
表示甲击中目标时射击的次数,求 的数学期望
的数学期望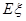 .(结果可以用分数表示)
.(结果可以用分数表示)