在真空中速度为v0=6.4×107m／s的电子束连续地射人两平行极板之间.极板长L=8.0×10-2m，间距d=5.0×10-3m，两极板不带电时，电子束将沿两极板之间的中线通过，在两极板加一个50Hz的交变电压U=U0sinωt，如果所加电压的最大值U0超过某一值Uc时，将开始出现以下现象：电子束有时能通过两极板，有时间断不能通过.(电子的质量为9.1×10-31kg)
求：(1)Uc的大小；
(2)U0为何值时才能使通过的时间t1跟间断的时间t2之比为t1：t2=2：1.
如图所示，长l＝0.8 m的细线上端固定在O点，下端连结一个质量为m＝0.4 kg的小球，悬点O距地面的高度H＝3.55 m，开始时将小球提到O点而静止，然后让它自由下落，当小球到达使细线被拉直的位置时，刚好把细线拉断，再经过t＝0.5 s落到地面，如果不考虑细线的形变，g＝10 m/s2，试求：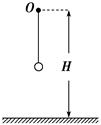
(1)细线拉断前后的速度大小和方向；
(2)假设细线由拉直到断裂所经历的时间为0.1 s，试确定细线的平均张力大小．
高速公路上甲、乙两车在同一车道上同向行驶，甲车在前，乙车在后，速度均为v0=30m/s，距离s0=100m，t=0时刻甲车遇紧急情况后，甲、乙两车的加速度随时间变化如图所示，取运动方向为正方向。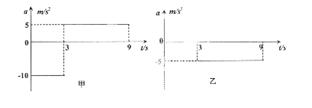
（1）通过计算说明两车在0～9s内会不会相撞？
（2）在一个坐标系中画出甲乙的速度时间图象。
如图所示，坐标系xOy在竖直平面内，空间有沿水平方向垂直于纸面向外的匀强磁场，磁感应强度大小为B,在x>0的空间里有沿x轴正方向的匀强电场，场强的大小为E，一个带正电的小球经过图中的x轴上的A点，沿着与水平方向成
= 300角的斜向下直线做匀速运动，经过y轴上的B点进人x<0的区域，要使小球进入x<0区域后能在竖直面内做匀速圆周运动，需在x<0区域另加一匀强电场，若带电小球做圆周运动通过x轴上的C点，且
，设重力加速度为g，求：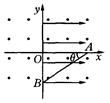
(1)小球运动速率的大小；
(2)小球从B点运动到C点所用时间及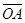
的长度．
如图所示，在以坐标原点O为圆心、半径为R的半圆形区域内，有相互垂直的匀强电场和匀强磁场，磁感应强度为B，磁场方向垂直于xOy平面向里。一带正电的粒子（不计重力）从O点沿y轴正方向以某一速度射入，带电粒子恰好做匀速直线运动，经t0时间从P点射出。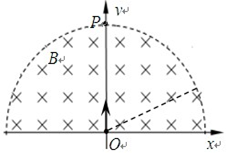
(1)求电场强度的大小和方向。
(2)若仅撤去磁场，带电粒子仍从O点以相同的速度射入，经
时间恰从半圆形区域的边界射出。求粒子运动加速度的大小。
(3)若仅撤去电场，带电粒子仍从O点射入，且速度为原来的4倍，求粒子在磁场中运动的时间。
如图所示，两根足够长的光滑金属导轨ab、cd竖直放置，导轨间距离为 L1电阻不计。在导轨上端并接两个额定功率均为P、电阻均为R的小灯泡。整个系统置于匀强磁场中，磁感应强度方向与导轨所在平面垂直。现将一质量为m、电阻可以忽略的金属棒MN从图示位置由静止开始释放。金属棒下落过程中保持水平，且与导轨接触良好。已知某时刻后两灯泡保持正常发光。重力加速度为g。求：
(1)磁感应强度的大小
(2)灯泡正常发光时导体棒的运动速率