(本小题满分10分)
求下列函数的导数:
(1)
(2)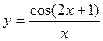
在△ABC中,角A,B,C的对边分别为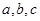 ,且
,且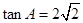 .
.
(Ⅰ)求sin2A;(Ⅱ)若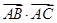 =4,且
=4,且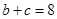 ,求
,求 .
.
已知 (其中
(其中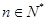 )
)
(1)求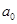 及
及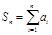 ;
;
(2)试比较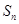 与
与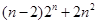 的大小,并说明理由.
的大小,并说明理由.
在1,2,---,7这7个自然数中,任取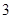 个不同的数.
个不同的数.
(1)求这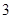 个数中至少有
个数中至少有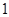 个是偶数的概率;
个是偶数的概率;
(2)设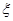 为这
为这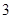 个数中两数相邻的组数(例如:若取出的数为
个数中两数相邻的组数(例如:若取出的数为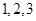 ,则有两组相邻的数
,则有两组相邻的数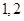 和
和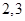 ,此时
,此时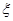 的值是
的值是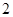 ).求随机变量
).求随机变量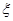 的分布列及其数学期望
的分布列及其数学期望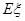 .
.
选修4-4:坐标系与参数方程
已知曲线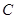 的参数方程为
的参数方程为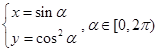 ,曲线
,曲线 的极坐标方程为
的极坐标方程为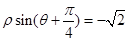 .
.
(1)将曲线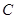 的参数方程化为普通方程;
的参数方程化为普通方程;
(2)曲线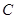 与曲线
与曲线 有无公共点?试说明理由.
有无公共点?试说明理由.
选修4-2:矩阵与变换
若点A(-2,2)在矩阵 对应变换的作用下得到的点为B(2,2),求矩阵
对应变换的作用下得到的点为B(2,2),求矩阵 .
.