((本小题满分12分)
已知圆C:x2+(y-1)2 =5,直线l:mx-y+l-m=0,
(1)求证:对任意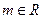 ,直线l与圆C总有两个不同的交点。
,直线l与圆C总有两个不同的交点。
(2)设l与圆C交于A、B两点,若| AB | = 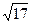 ,求l的倾斜角;
,求l的倾斜角;
(3)求弦AB的中点M的轨迹方程;
已知 ,
,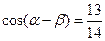 ,且
,且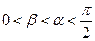 ,
,
(1)求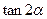 (2)求
(2)求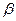
(1)已知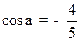 ,且
,且 为第
为第 三象限角,求
三象限角,求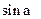 的值
的值
(2)已知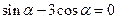 ,计算
,计算 的值
的值
(本小题满分1 2分)
2分)
已知函数  ,
, .
.
(Ⅰ)当  时,求函数
时,求函数  的最小值;
的最小值;
(Ⅱ)当  时,讨论函数
时,讨论函数  的单调性;
的单调性;
(Ⅲ)求证:当  时,对任意的
时,对任意的 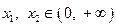 ,且
,且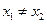 ,有
,有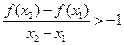 .
.
(本小题满分12分)
已知直线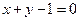 与椭圆
与椭圆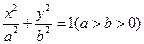 相交于
相交于 、
、 两点,
两点, 是线段
是线段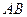 上
上
的一点, ,且点M在直线
,且点M在直线 上,
上,
(Ⅰ)求椭 圆的离心率;
圆的离心率;
(Ⅱ)若椭圆的焦点关于直线 的对称点在单位圆
的对称点在单位圆 上,求椭圆的方程。
上,求椭圆的方程。
(本小题满分12分)
已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,AC∥DE,AC与BD相交于H点
(Ⅰ)求证:BD 平分∠ABC
平分∠ABC
(Ⅱ)若AB=4,AD=6,BD=8,求AH的长