如图,在四棱锥P—ABCD中,底面ABCD是矩形,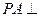 平面ABCD,PA=AD=2,AB=1,
平面ABCD,PA=AD=2,AB=1,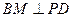 于点M.
于点M.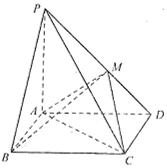
(1)求证: ;
;
(2)求直线CD与平面ACM所成的角的余弦值.
已知等差数列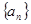 中,
中, ,
,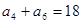 .
.
(Ⅰ)求数列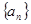 的通项公式;
的通项公式;
(Ⅱ)若数列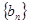 满足:
满足: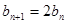 ,并且
,并且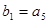 ,试求数列
,试求数列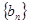 的前
的前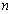 项和
项和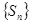 .
.
已知 ;
; 若
若 是
是 的必要非充分条件,求实数
的必要非充分条件,求实数 的取值范围。
的取值范围。
(本小题满分12分)
已知函数f(x)=Asin(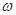 x+
x+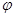 )(x∈R,
)(x∈R,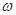 >0, 0<
>0, 0<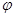 <
<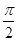 )的部分图象如图所示。
)的部分图象如图所示。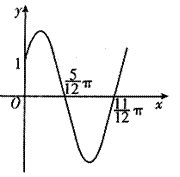
(1)求函数f(x)的解析式;
(2)求函数g(x)=f(x- )的单调递增区间。
)的单调递增区间。
(本小题满分12分)
已知函数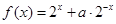 是定义域为
是定义域为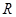 的奇函数,(1)求实数
的奇函数,(1)求实数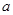 的值;(2)证明
的值;(2)证明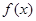 是
是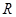 上的单调函数;(3)若对于任意的
上的单调函数;(3)若对于任意的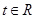 ,不等式
,不等式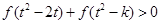 恒成立,求
恒成立,求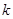 的取值范围.
的取值范围.
(本小题满分12分)
某企业生产A,B两种产品,根据市场调查与预测,A产品的利润与投资成正比,其关系如图1;B产品的利润与投资的算术平方根成正比,其关系如图2(注:利润和投资单位:万元).
(1)分别将A、B两种产品的利润表示为投资的函数关系式;
(2)已知该企业已筹集到18万元资金,并将全部投入A,B两种产品的生产.
①若平均投入生产两种产品,可获得多少利润?
②问:如果你是厂长,怎样分配这18万元投资,才能使该企业获得最大利润?其最大利润约为多少万元?