(本小题满分12分)
某学校要用鲜花布置花圃中 五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.
五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.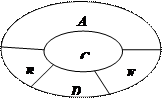
(1)当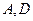 区域同时用红色鲜花时,求布置花圃的不同方法的种数;
区域同时用红色鲜花时,求布置花圃的不同方法的种数;
(2)求恰 有两个区域用红色鲜花的概率;
有两个区域用红色鲜花的概率;
(3)记 为花圃中用红色鲜花布置的区域的个数,求随机变量
为花圃中用红色鲜花布置的区域的个数,求随机变量 的分布列及其数学期望
的分布列及其数学期望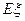 .
.
(本小题满分12分)已知等差数列 的首项
的首项 ,公差
,公差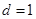 ,前
,前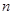 项和为
项和为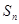 ,
, ,
,
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 前
前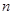 项和为
项和为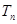 ,求
,求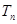
(本小题满分10分) 选修4—5:不等式选讲已知关于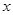 的不等式
的不等式 ,其解集为
,其解集为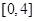 .
.
(Ⅰ)求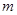 的值;
的值;
(Ⅱ)若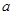 ,
, 均为正实数,且满足
均为正实数,且满足 ,求
,求 的最小值.
的最小值.
(本小题满分10分) 选修4—4:坐标系与参数方程
已知极坐标系的极点在直角坐标系的原点处,极轴与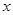 轴的正半轴重合,直线
轴的正半轴重合,直线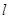 的极坐标方程为:
的极坐标方程为: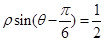 ,曲线
,曲线 的参数方程为:
的参数方程为:
(Ⅰ)写出直线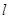 的直角坐标方程;
的直角坐标方程;
(Ⅱ)求曲线 上的点到直线
上的点到直线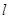 的距离的最大值.
的距离的最大值.
(本小题满分12分)已知椭圆 的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线
的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线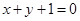 与以椭圆
与以椭圆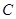 的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.
的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.
(Ⅰ)求椭圆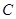 的方程;
的方程;
(Ⅱ)设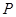 为椭圆
为椭圆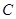 上一点,若过点
上一点,若过点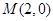 的直线
的直线 与椭圆
与椭圆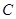 相交于不同的两点
相交于不同的两点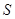 和
和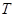 ,满足
,满足 (
(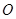 为坐标原点),求实数
为坐标原点),求实数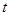 的取值范围.
的取值范围.
(本小题满分12分)如图,已知四棱锥 的底面为菱形,
的底面为菱形, ,
,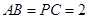 ,
, .
.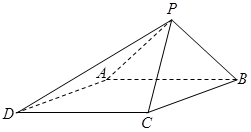
(Ⅰ)求证: ;
;
(Ⅱ)求二面角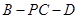 的余弦值.
的余弦值.