如图,己知 中,
中,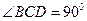 ,
,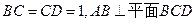 ,
, 且
且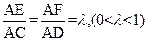
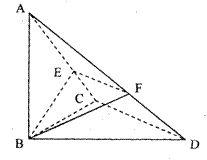
(1)求证:不论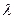 为何值,总有
为何值,总有
(2)若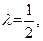 求三棱锥
求三棱锥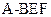 的体积.
的体积.
在 中,角A、B、C的对边分别是a、b、c,若
中,角A、B、C的对边分别是a、b、c,若 .
.
(1)求内角B的大小;
(2)若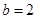 ,求
,求 面积的最大值.
面积的最大值.
已知数列 中,
中, ,
,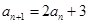 ,数列
,数列 中,
中,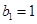 ,且点
,且点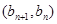 在直线
在直线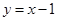 上.
上.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的通项公式;
的通项公式;
(3)若 ,求数列
,求数列 的前n项和
的前n项和 .
.
.如图所示,已知A、B两点的距离为100海里,B在A的北偏东30°处,甲船自A以50海里/小时的速度向B航行,同时乙船自B以30海里/小时的速度沿方位角150°方向航行.问航行几小时两船之间的距离最短?
如果有穷数列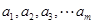 (
(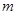 为正整数)满足条件
为正整数)满足条件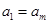 ,
,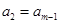 ,…,
,…,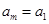 ,即
,即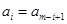 (
(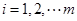 ),我们称其为“对称数列”.例如,数列1,2,5,2,1与数列8,4,2,2,4,8都是“对称数列”.
),我们称其为“对称数列”.例如,数列1,2,5,2,1与数列8,4,2,2,4,8都是“对称数列”.
(1)设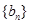 是7项的“对称数列”,其中
是7项的“对称数列”,其中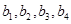 是等差数列,且
是等差数列,且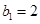 ,
,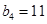 .依次写出
.依次写出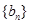 的每一项;
的每一项;
(2)设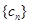 是49项的“对称数列”,其中
是49项的“对称数列”,其中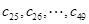 是首项为1,公比为2的等比数列,求
是首项为1,公比为2的等比数列,求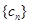 各项的和S.
各项的和S.
在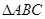 中,已知
中,已知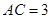 ,
,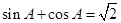 ,
,
(1)求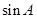 的值;
的值;
(2)若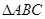 的面积
的面积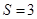 ,求BC的值.
,求BC的值.