（如图，在边长为a的菱形ABCD中，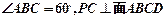
，E,F是PA和AB的中点。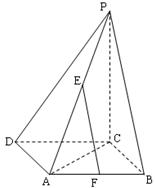
（1）求证： EF||平面PBC ;
（2）求E到平面PBC的距离。
(本题满分12分)已知函数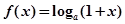
，
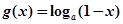，其中
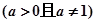,设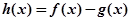
．
(1)判断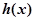
的奇偶性，并说明理由；
(2)若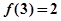
，求使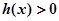
成立的x的集合。
在正四棱柱ABCD－A1B1C1D1中，E为CC1的中点．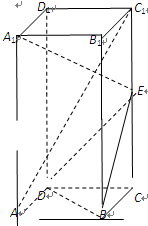
（1）求证：AC1∥平面BDE；（2）求异面直线A1E与BD所成角。
求过直线2x+3y+5=O和直线2x+5y+7=0的交点，且与直线x+3y=0平行的直线的方程，并求这两条平行线间的距离。
已知函数
在定义域
上为增函数，且满足
(1)求
的值 (2)解不等式
设集合P={1，2，3}和Q={－1，1，2，3，4}，分别从集合P和Q中随机取一个数作为
和
组成数对（
,并构成函数
（Ⅰ）写出所有可能的数对(，并计算
，且
的概率；
（Ⅱ）求函数
在区间[
上是增函数的概率.