已知函数 在定义域
在定义域 上为增函数,且满足
上为增函数,且满足
(1)求 的值 (2)解不等式
的值 (2)解不等式
(本小题满分14分)
已知 是等比数列,
是等比数列, ,
, ;
; 是等差数列,
是等差数列, ,
,
 .
.
(Ⅰ) 求数列 的前
的前 项和
项和 的公式;
的公式;
(Ⅱ) 求数列 的通项公式;
的通项公式; ,其中
,其中 ,试比较
,试比较 与
与 的大小,并证明你的结论.
的大小,并证明你的结论.
(本小题满分14分)
已知圆 方程为:
方程为: .
.
(Ⅰ)直线 过点
过点 ,且与圆
,且与圆 交于
交于 、
、 两点,若
两点,若 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)过圆 上一动点
上一动点 作平行于
作平行于 轴的直线
轴的直线 ,设
,设 与
与 轴的交点为
轴的交点为 ,若向量
,若向量 ,求动点
,求动点 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
(本小题满分14分)
如图:四棱锥P—ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD= ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
(Ⅰ)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(Ⅱ)证明:无论点E在BC边的何处,都有PE⊥AF;
(Ⅲ)当BE等于何值时,PA与平面PDE所成角的大小为45°
(本小题满分12分) 
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
(Ⅰ)估计这次测试数学成绩的平均分;
(Ⅱ)假设在[90,100]段的学生的数学成绩都不相同,且都在94分以上,现用简单随机抽样的方法,从95,96,97,98,99,100这6个数中任取2个数,求这两个数恰好是在[90,100]段的两个学生的数学成绩的概率.
(本小题满分12分)
已知函数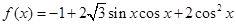
(Ⅰ)求函数f (x)的最小正周期;
(Ⅱ)求函数f (x)的单调减区间.