(本小题满分16分)
如图,在平面直角坐标系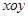 中,已知点
中,已知点 为椭圆
为椭圆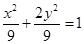 的右顶点, 点
的右顶点, 点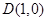 ,点
,点 在椭
在椭
圆上,  .
.
(1)求直线 的方程;
的方程;
(2)求直线 被过
被过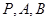 三点的圆
三点的圆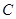 截得的弦长;
截得的弦长;
(3)是否存在分别以 为弦的两个相外切的等圆?若存在,求出这两个圆的方程;若不存在,请说明理由.
为弦的两个相外切的等圆?若存在,求出这两个圆的方程;若不存在,请说明理由.
(本小题满分14分)已知数列 的相邻两项
的相邻两项 是关于
是关于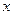 的方程
的方程 的两实根,且
的两实根,且

(1)求证:数列 是等比数列;
是等比数列;
(2)设 是数列
是数列 的前
的前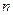 项和,求
项和,求 ;
;
(3)问是否存在常数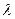 ,使得
,使得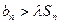 对
对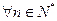 都成立,若存在,求出
都成立,若存在,求出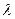 的取值范围,若不存在,请说明理由。
的取值范围,若不存在,请说明理由。
(本小题满分14分)如图所示,椭圆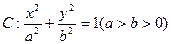 的离心率为
的离心率为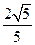 ,且A(0,1)是椭圆C的顶点。
,且A(0,1)是椭圆C的顶点。
(1)求椭圆C的方程;
(2)过点A作斜率为1的直线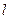 ,在直线
,在直线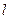 上求一点M,使得以椭圆C的焦点为焦点,且过点M的双曲线E的实轴最长,并求此双曲线E的方程。
上求一点M,使得以椭圆C的焦点为焦点,且过点M的双曲线E的实轴最长,并求此双曲线E的方程。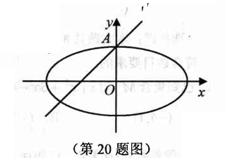
已知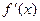 是
是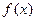 的导函数,
的导函数,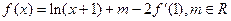 ,且函数
,且函数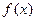 的图象过点(0,-2)。
的图象过点(0,-2)。
(1)求函数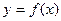 的表达式;
的表达式;
(2)设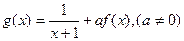 ,若
,若 在定义域内恒成立,求实数
在定义域内恒成立,求实数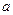 的取值范围。
的取值范围。
(本小题满分14分)已知四棱锥P—ABCD的三视图如右图所示,
其中正(主)视图与侧(左)视为直角三角形,俯视图为正方形。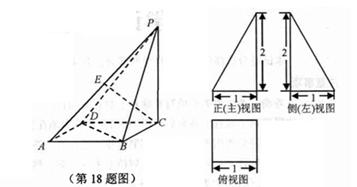 (1)求四棱锥P—ABCD的体积;
(1)求四棱锥P—ABCD的体积; (2)若E是侧棱
(2)若E是侧棱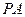 上的动点。问:不论点E在PA的
上的动点。问:不论点E在PA的
任何位置上,是否都有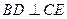 ?
?
请证明你的结论?
(3)求二面角D—PA—B的余弦值。
(本小题满分12分)第16届亚运会将于2010年11月12日至27日在中国广州进行,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余不喜爱。
(1)根据以上数据完成以下2×2列联表:
| 喜爱运动 |
不喜爱运动 |
总计 |
|
| 男 |
10 |
16 |
|
| 女 |
6 |
14 |
|
| 总计 |
30 |
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关?
(3)从女志原者中抽取2人参加接待工作,若其中喜爱运动的人数为 ,求
,求 的分布列和均值。
的分布列和均值。
参考公式: ,其中
,其中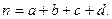
参考数据:
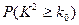 |
0.40 |
0.25 |
0.10 |
0.010 |
 |
0.708 |
1.323 |
2.706 |
6.635 |