(本小题满分14分)
某商店经销一种奥运会纪念品,每件产品的成本为30元,并且每卖出一件产品需向税务部门上交 元(
元( 为常数,2≤a≤5 )的税收.设每件产品的售价为x元(35≤x≤41),根据市场调查,日销售量与
为常数,2≤a≤5 )的税收.设每件产品的售价为x元(35≤x≤41),根据市场调查,日销售量与 (e为自然对数的底数)成反比例.已知每件产品的日售价为40元时,日销售量为10件.
(e为自然对数的底数)成反比例.已知每件产品的日售价为40元时,日销售量为10件.
(1)求该商店的日利润L(x)元与每件产品的日售价x元的函数关系式;
(2)当每件产品的日售价为多少元时,该商品的日利润L(x)最大,并求出L(x)的最大值.
某校在两个班进行教学方式对比试验,两个月后进行了一次检测,试验班与对照班成绩统计如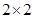 列联表所示(单位:人).
列联表所示(单位:人).
⑴ 求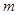 ,
,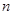 ;
;
⑵ 你有多大把握认为“教学方式与成绩有关系”?
| 80及80分以上 |
80分以下 |
合计 |
|
| 试验班 |
35 |
15 |
50 |
| 对照班 |
20 |
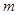 |
50 |
| 合计 |
55 |
45 |
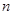 |
参考公式及数据: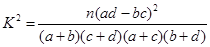 ,其中
,其中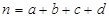 为样本容量.
为样本容量.
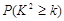 |
… |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
… |
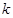 |
… |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
… |
已知数列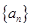 的前
的前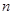 项和
项和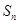 满足
满足 ,且
,且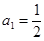 .
.
⑴ 求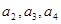 的值;
的值;
⑵ 猜想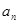 的表达式(不必证明)
的表达式(不必证明)
已知复数 .
.
⑴ 求 的实部与虚部; ⑵ 若
的实部与虚部; ⑵ 若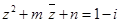 (
(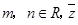 是
是 的共轭复数),求
的共轭复数),求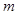 和
和 的值.
的值.
已知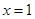 是函数
是函数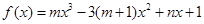 的一个极值点,其中
的一个极值点,其中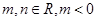 .(I)求
.(I)求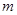 与
与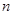 的关系式;(II)求
的关系式;(II)求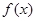 的单调区间
的单调区间
已知函数
(Ⅰ)求 的单调减区间;
的单调减区间;
(Ⅱ)若 在区间[-2,2].上的最大值为20,求它在该区间上的最小值
在区间[-2,2].上的最大值为20,求它在该区间上的最小值