已知函数
(Ⅰ)求 的单调减区间;
的单调减区间;
(Ⅱ)若 在区间[-2,2].上的最大值为20,求它在该区间上的最小值
在区间[-2,2].上的最大值为20,求它在该区间上的最小值
(本小题10分)△ABC中,D在边BC上,且BD=2,DC=1,∠B=60o,∠ADC=150o,求AC的长及△ABC的面积.
(本小题满分12分)
如图,设矩形ABCD(AB>AD)的周长为24,把它关于AC折起来,AB折过去后,交DC于点P. 设AB="x," 求△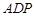 的最大面积及相应的x值.
的最大面积及相应的x值.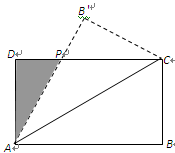
(本小题满分12分)
如图,在四边形ABCD中,AC平分∠DAB,∠ABC=600,AC=7,AD=6,S△ADC=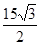 ,
,
求AB的长.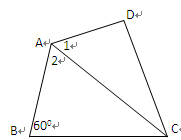
(本小题满分12分)
已知集合 ,
,
求实数a的取值范围。
(本小题满分12分)
已知等差数列{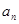 }的前n项和为Sn,且
}的前n项和为Sn,且
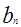 =
=
(1)求通项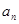 ;
;
(2)求数列{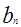 }的前n项和的最小值。
}的前n项和的最小值。