(本小题满分13分)
已知函数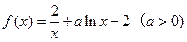 .
.
(Ⅰ)若曲线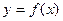 在点
在点 处的切线与直线
处的切线与直线 垂直,求函数
垂直,求函数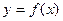 的单调区间;
的单调区间;
(Ⅱ)若对于 都有
都有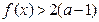 成立,试求
成立,试求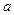 的取值范围;
的取值范围;
(Ⅲ)记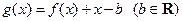 .当
.当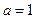 时,函数
时,函数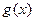 在区间
在区间 上有两个零点,求实数
上有两个零点,求实数 的取值范围.
的取值范围.
已知直三棱柱ABC-A1B1C1的侧棱长与
底面三角形的各边长都等于a,点D为BC的中点.
求证:(1)平面AC1D⊥平面BCC1B1;
(2)A1B∥平面AC1D.(3)求二面角C1-DA-C的大小.
(本小题满分14分)设椭圆C1的方程为 (a>b>0),曲线C2的方程为y=
(a>b>0),曲线C2的方程为y= ,且曲线C1与C2在第一象限内只有一个公共点P。(1)试用a表示点P的坐标;(2)设A、B是椭圆C1的两个焦点,当a变化时,求△ABP的面积函数S(a)的值域;(3)记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个。设g(a)是以椭圆C1的半焦距为边长的正方形的面积,试求函数f(a)=min{g(a), S(a)}的表达式。
,且曲线C1与C2在第一象限内只有一个公共点P。(1)试用a表示点P的坐标;(2)设A、B是椭圆C1的两个焦点,当a变化时,求△ABP的面积函数S(a)的值域;(3)记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个。设g(a)是以椭圆C1的半焦距为边长的正方形的面积,试求函数f(a)=min{g(a), S(a)}的表达式。
(本小题满分12分)学校餐厅每天供应1000名学生用餐,每星期一有A、B两样特色菜可供选择(每个学生都将从二者中选一),调查资料表明,凡是在本周星期一选A菜的,下周星期一会有20%改选B,而选B菜的,下周星期一则有30%改选A,若用A 、B
、B 分别表示在第n个星期一选A、B菜的人数。(1)试以A
分别表示在第n个星期一选A、B菜的人数。(1)试以A 表示A
表示A ;(2)若A
;(2)若A =200,求{A
=200,求{A }的通项公式;(3)问第n个星期一时,选A与选B的人数相等?
}的通项公式;(3)问第n个星期一时,选A与选B的人数相等?
(本小题满分12分)已知四棱锥P—ABCD,
底面ABCD是菱形, 平面ABCD,PD=AD,点E为AB中点,点F为PD中点。(1)证明平面PED⊥平面PAB;(2)求二面角P—AB—F的平面角的余弦值。
平面ABCD,PD=AD,点E为AB中点,点F为PD中点。(1)证明平面PED⊥平面PAB;(2)求二面角P—AB—F的平面角的余弦值。
(本小题满分12分)为应对金融危机,刺激消费,某市给市民发放面额为100元 的旅游消费卷,由抽样调查预计老、中、青三类市民持有这种消费卷到某旅游景点消费额及其概率如下表:
的旅游消费卷,由抽样调查预计老、中、青三类市民持有这种消费卷到某旅游景点消费额及其概率如下表:
  |
200元 |
300元 |
400元 |
500元 |
| 老年 |
0.4 |
0.3 |
0.2 |
0.1 |
| 中年 |
0.3 |
0.4 |
0.2 |
0.1 |
| 青年 |
0.3 |
0.3 |
0.2 |
0.2 |
某天恰好有持有这种消费卷的老年人、中年人、青年人各一人到该旅游景点,(1)求这三人恰有两人消费额不少于300元的概率;(2)求这三人消费总额大于或等于1300元的概率。