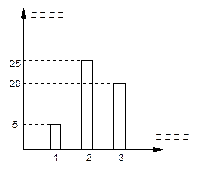.在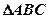 中,
中,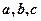 分别是角
分别是角 的对边,向量
的对边,向量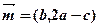 ,
,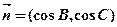 ,且
,且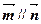 .
.
(1)求角 的大小;
的大小;
(2)设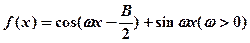 ,且
,且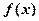 的最小正周期为
的最小正周期为 ,求
,求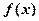 在区间
在区间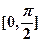 上的最大值和最小值.
上的最大值和最小值.
已知椭圆C的中心在原点,焦点在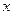 轴上,长轴长是短轴长的
轴上,长轴长是短轴长的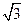 倍,其上一点到右焦点的最短距离为
倍,其上一点到右焦点的最短距离为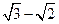 .
.
(1)求椭圆C的标准方程;
(2)若直线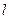 :
: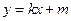 与圆O:
与圆O: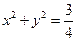 相切,且交椭圆C于A、B两点,
相切,且交椭圆C于A、B两点, 求当△AOB的面积最大时直线
求当△AOB的面积最大时直线 的方程.
的方程.
已知数列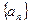 中
中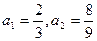 .当
.当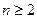 时
时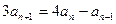 .(
.(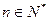 )
)
(Ⅰ)证明: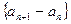 为等比数列;
为等比数列;
(Ⅱ) 求数列
求数列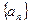 的通项;
的通项;
(Ⅲ)若数列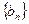 满足
满足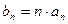 ,求
,求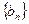 的前
的前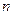 项和
项和 .
.
已知四棱锥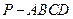 的三视图如下图所示,
的三视图如下图所示,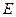 是侧棱
是侧棱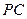 上的动点.
上的动点.
(1) 求四棱锥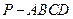 的体积;
的体积;
(2) 是否不论点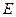 在何位置,都有
在何位置,都有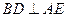 ?证明你的结论;
?证明你的结论;
(3) 若点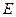 为
为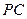 的中点,求二面角
的中点,求二面角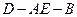 的大小.
的大小.
已知 .
.
(Ⅰ)若函数 在
在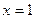 处的切线与直线
处的切线与直线 垂直,且
垂直,且 ,求函数
,求函数 的解析式;
的解析式;
(Ⅱ)若 在区间
在区间 上单调递减,求
上单调递减,求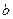 的取值范围.
的取值范围.
西安市某中学号召学生在2010年春节期间至少参加一次社会公益活动.经统计,该校高三(1)班共50名学生参加公益活动情况如图所示.
(Ⅰ)从高三(1)班任选两名学生,求他们参加活动次数恰好相等的概率;
(Ⅱ)从高三(1)班任选两名学生,用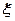 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量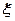 的分布列及均值
的分布列及均值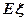 .
.