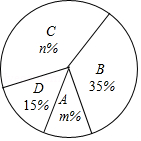
某校为了推进学校均衡发展,计划再购进一批图书,丰富学生的课外阅读.为了解学生对课外阅读的需求情况,学校对学生所喜爱的读物:
.文学,
.艺术,
.科普,
.生活,
.其他,进行了随机抽样调查(规定每名学生只能选其中一类读物),并将调查结果绘制成以下不完整的统计图表.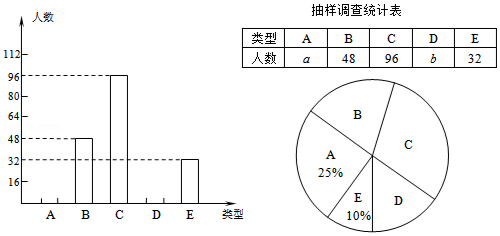
(1) , ,请补全条形统计图;
(2)如果全校有2500名学生,请你估计全校有多少名学生喜爱科普读物;
(3)学校从喜爱科普读物的学生中选拔出2名男生和3名女生,并从中随机抽取2名学生参加科普知识竞赛,请你用树状图或列表法求出恰好抽到一名男生和一名女生的概率.
如图,若要在宽 为20米的城南大道两边安装路灯,路灯的灯臂 长2米,且与灯柱 成 角,路灯采用圆锥形灯罩,灯罩的轴线 与灯臂 垂直,当灯罩的轴线 通过公路路面的中心线时照明效果最好,此时,路灯的灯柱 高应该设计为多少米(结果保留根号)?

如图,在边长为1的正方形网格中建立平面直角坐标系,已知 三个顶点分别为 、 、 .
(1)画出 关于 轴对称的△ ;
(2)以原点 为位似中心,在 轴的上方画出△ ,使△ 与 位似,且位似比为2,并求出△ 的面积.

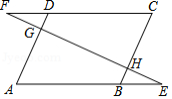
如右图,在 中, 、 分别是 、 延长线上的点,且 ,连接 交 、 于点 、 .求证: .
今年5月份,我市某中学开展争做“五好小公民”征文比赛活动,赛后随机抽取了部分参赛学生的成绩,按得分划分为 , , , 四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
|
等级 |
成绩 |
频数(人数) |
|
|
|
4 |
|
|
|
|
|
|
|
16 |
|
|
|
6 |
根据以上信息,解答以下问题:
(1)表中的 ;
(2)扇形统计图中 , , 等级对应的扇形的圆心角为 度;
(3)该校准备从上述获得 等级的四名学生中选取两人做为学校“五好小公民”志愿者,已知这四人中有两名男生(用 , 表示)和两名女生(用 , 表示),请用列表或画树状图的方法求恰好选取的是 和 的概率.