((本小题满分12分)
现将边长为2米的正方形铁片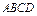 裁剪成一个半径为1米的扇形
裁剪成一个半径为1米的扇形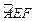 和一个矩形
和一个矩形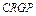 ,如图所示,点
,如图所示,点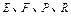 分别在
分别在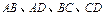 上,点
上,点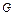 在
在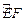 上.设矩形
上.设矩形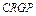 的面积为
的面积为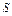 ,
, ,试将
,试将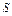 表示为
表示为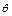 的函数,并指出点
的函数,并指出点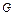 在
在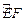 的何处时,矩形面积最大,并求之.
的何处时,矩形面积最大,并求之.
在平面直角坐标系 中,已知圆
中,已知圆 和圆
和圆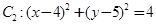 .
.
(1)若直线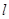 过点
过点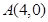 ,且被圆
,且被圆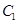 截得的弦长为
截得的弦长为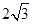 ,求直线
,求直线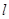 的方程;
的方程;
(2)设 为平面上的点,满足:存在过点
为平面上的点,满足:存在过点 的无穷多对互相垂直的直线
的无穷多对互相垂直的直线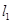 和
和 ,它们分别与圆
,它们分别与圆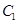 和圆
和圆 相交,且直线
相交,且直线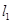 被圆
被圆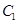 截得的弦长与直线
截得的弦长与直线 被圆
被圆 截得的弦长相等,试求所有满足条件的点
截得的弦长相等,试求所有满足条件的点 的坐标.
的坐标.
如图,已知在四棱锥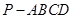 中,底面
中,底面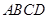 是矩形,
是矩形, 平面
平面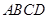 ,
, 、
、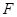 分别是
分别是 、
、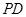 的中点.
的中点.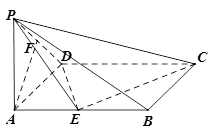
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)若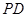 与平面
与平面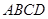 所成角为
所成角为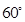 ,且
,且 ,求点
,求点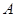 到平面
到平面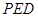 的距离.
的距离.
已知函数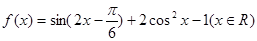
(1)求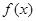 的单调递增区间;
的单调递增区间;
(2)在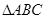 中,内角A,B,C的对边分别为
中,内角A,B,C的对边分别为 ,已知
,已知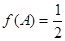 ,
,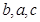 成等差数列,且
成等差数列,且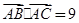 ,求边
,求边 的值.
的值.
相关部门对跳水运动员进行达标定级考核,动作自选,并规定完成动作成绩在八分及以上的定为达标,成绩在九分及以上的定为一级运动员. 已知参加此次考核的共有56名运动员.
(1)考核结束后,从参加考核的运动员中随机抽取了8人,发现这8人中有2人没有达标,有3人为一级运动员,据此请估计此次考核的达标率及被定为一级运动员的人数;
(2)经过考核,决定从其中的A、B、C、D、E五名一级运动员中任选2名参加跳水比赛(这五位运动员每位被选中的可能性相同). 写出所有可能情况,并求运动员E被选中的概率.
已知等差数列 的前
的前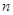 项和为
项和为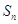 ,
,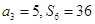 .
.
(1)求数列 的通项公式;
的通项公式;
(2) 设 ,求数列
,求数列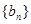 的前
的前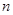 项和
项和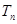 .
.