((本小题满分14分)
已知函数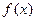 满足
满足 当
当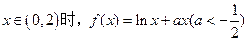 ,当
,当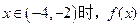 的最大值为
的最大值为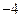 。
。
(1)求 时函数
时函数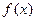 的解析式;
的解析式;
(2)是否存在实数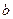 使得不等式
使得不等式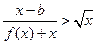 对于
对于 若存在,求出实数
若存在,求出实数 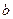 的取值集合,若不存在,说明理由.
的取值集合,若不存在,说明理由.
设 是首项为
是首项为 ,公差为
,公差为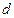 的等差数列(d≠0),
的等差数列(d≠0),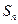 是其前
是其前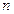 项和.记bn=
项和.记bn=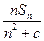 ,
, ,其中
,其中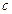 为实数.
为实数.
(1) 若 ,且
,且 ,
, ,
, 成等比数列,证明:Snk=n2Sk(k,n∈N+);
成等比数列,证明:Snk=n2Sk(k,n∈N+);
(2) 若 是等差数列,证明:
是等差数列,证明: .
.
设数列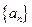 的前
的前 项和为
项和为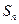 .已知
.已知 ,
,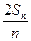 =an+1-
=an+1-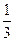 n2-n-
n2-n-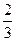 (
(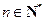 )
)
(1) 求 的值;
的值;
(2) 求数列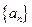 的通项公式;
的通项公式;
(3) 证明:对一切正整数 ,有
,有 +
+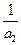 +…+
+…+ <
<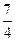 .
.
已知等差数列{an}满足a2=0,a6+a8=-10
(1)求数列{an}的通项公式;
(2)求数列{ }的前n项和.
}的前n项和.
已知函数f(x)=(2cos2x-1)sin2x+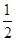 cos4x
cos4x
(1)求f(x)的最小正周期及最大值。
(2)设A,B,C为△ABC的三个内角,若cosB=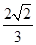 ,f(
,f(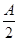 )=-
)=-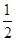 ,且角A为钝角,求sinC
,且角A为钝角,求sinC
已知抛物线C1:x2=y,圆C2:x2+(y-4)2=1的圆心为点M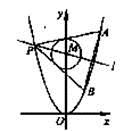
(1)求点M到抛物线C1的准线的距离;
(2)已知点P是抛物线C1上一点(异于原点),过点P作圆C2的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求直线l的方程