(本小题14分)已知函数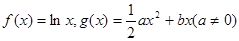
(Ⅰ)若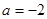 时,函数
时,函数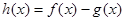 在其定义域上是增函数,求b的取值范围;
在其定义域上是增函数,求b的取值范围;
(Ⅱ)在(Ⅰ)的结论下,设函数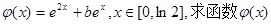 的最小值;
的最小值;
(Ⅲ)设函数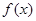 的图象C1与函数
的图象C1与函数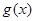 的图象C2交于P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
的图象C2交于P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
(本小题14分)设 是定义在
是定义在 上的奇函数,函数
上的奇函数,函数 与
与 的图象关于
的图象关于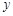 轴对称,且当
轴对称,且当 时,
时,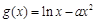 .
.
(1)求函数 的解析式;
的解析式;
(2)若对于区间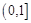 上任意的
上任意的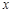 ,都有
,都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
在某次水下考古活动中,需要潜水员潜入水深为30米的水底进行作业.其用氧量包含3个方面:①下潜时,平均速度为 (米/单位时间),单位时间内用氧量为
(米/单位时间),单位时间内用氧量为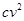 (
(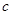 为正常数);②在水底作业需5个单位时间,每个单位时间用氧量为0.4;③返回水面时,平均速度为
为正常数);②在水底作业需5个单位时间,每个单位时间用氧量为0.4;③返回水面时,平均速度为 (米/单位时间), 单位时间用氧量为0.2.记该潜水员在此次考古活动中,总用氧量为
(米/单位时间), 单位时间用氧量为0.2.记该潜水员在此次考古活动中,总用氧量为 .
.
(1)将 表示为
表示为 的函数;
的函数;
(2)设0< ≤5,试确定下潜速度
≤5,试确定下潜速度 ,使总的用氧量最少.
,使总的用氧量最少.
(本小题14分)已知四面体 中,
中,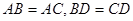 ,平面
,平面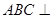 平面
平面 ,
,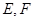 分别为棱
分别为棱 和
和 的中点。
的中点。
(1)求证: 平面
平面 ;
;
(2)求证: ;
;
(3)若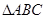 内的点
内的点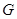 满足
满足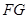 ∥平面
∥平面 ,设点
,设点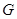 构成集合
构成集合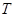 ,试描述点集
,试描述点集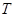 的位置(不必说明理由)
的位置(不必说明理由)
(本小题14分)如图,在平面直角坐标系 中,以
中,以 轴为始边做两个锐角
轴为始边做两个锐角 ,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
(1)求 的值;
的值;
(2)求 的值。
的值。