(本小题满分8分) 某校在高二年级开设了 ,
, ,
, 三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从
三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从 ,
, ,
, 三个兴趣小组的人员中,抽取若干人组成调查小组,有关数据见下表(单位:人)
三个兴趣小组的人员中,抽取若干人组成调查小组,有关数据见下表(单位:人)
| 兴趣小组 |
小组人数 |
抽取人数 |
 |
24 |
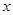 |
 |
36 |
3 |
 |
48 |
 |
(1)求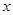 ,
, 的值;
的值;
(2)若从 ,
, 两个兴趣小组抽取的人中选2人作专题发言,求这2人都来自兴趣小组
两个兴趣小组抽取的人中选2人作专题发言,求这2人都来自兴趣小组 的概率.
的概率.
(本小题满分14分)
设数列 满足
满足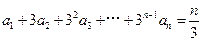 ,
, .
.
(Ⅰ)求数列 的通项;
的通项;
(Ⅱ)设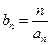 ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分12分)
从某批产品中,有放回地抽取产品二次,每次随机抽取1件,假设事件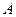 :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率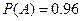 .
.
(1)求从该批产品中任取1件是二等品的概率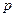 ;
;
(2)若该批产品共100件,从中任意抽取2件,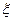 表示取出的2件产品中二等品的件数,求
表示取出的2件产品中二等品的件数,求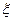 的分布列.
的分布列.
(本小题满分12分)已知函数 .
.
(Ⅰ)求函数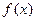 的最小正周期;
的最小正周期;
(Ⅱ)求函数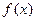 在区间
在区间 上的最小值和最大值.
上的最小值和最大值.
(本小题满分14分)
已知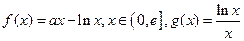 ,其中
,其中 是自然对数的底,
是自然对数的底,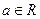

(1) 时,求
时,求 的单调区间、极值;
的单调区间、极值;
(2)是否存在实数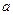 ,使
,使 的最小值是3,若存在,求出
的最小值是3,若存在,求出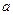 的值,若不存在,说明理由;
的值,若不存在,说明理由;
(3)在(1)的条件下,求证:

(本小题满分12分)已知数列{an}中,a1=2,前n项和为Sn,对于任意n≥2,
3Sn-4,an, 总成等差数列.
总成等差数列.
(I)求数列 通项公式an;
通项公式an;
(II)若数列 满足
满足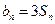 ,求数列
,求数列 的前n项和
的前n项和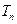 .
.