(本小题12分)
已知如下等式: ,
, ,
,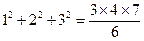 ,
,
当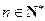 时,试猜想
时,试猜想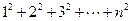 的值,并用数学归纳法给予证明。
的值,并用数学归纳法给予证明。
(本小题满分12分)在一个选拔项目中,每个选手都需要进行4轮考核,每轮设有一个问
题,能正确回答者进入下一轮考核,否则被淘汰。已知某选手能正确回答第一、二、三、
四轮问题的概率分别为 、
、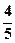 、
、 、
、 ,且各轮问题能否正确回答互不影响。
,且各轮问题能否正确回答互不影响。
(Ⅰ)求该选手进入第三轮才被淘汰的概率;
(Ⅱ)求该选手至多进入第三轮考核的概率;
(本小题满分10分)已知向量 ,
, 。
。
(Ⅰ)若 ,求
,求 的值;
的值;
(Ⅱ)设 ,求
,求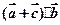 的取值范围.
的取值范围.
已知函数 .
.
(Ⅰ)若函数在区间 (其中
(其中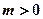 )上存在极值,求实数
)上存在极值,求实数 的取值范围;
的取值范围;
(Ⅱ)如果当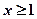 时,不等式
时,不等式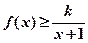 恒成立,求实数
恒成立,求实数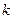 的取值范围;
的取值范围;
(Ⅲ)求证: .
.
已知椭圆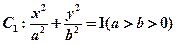 的离心率为
的离心率为 ,
,
直线 与以原点为圆心、以椭圆
与以原点为圆心、以椭圆 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设椭圆 的左焦点为F1,右焦点为F2,直线
的左焦点为F1,右焦点为F2,直线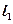 过点F1,且垂直于椭圆的长轴,动直线
过点F1,且垂直于椭圆的长轴,动直线 垂直
垂直 于点P,线段PF2的垂直平分线交
于点P,线段PF2的垂直平分线交 于点M,求点M的轨迹C2的方程;
于点M,求点M的轨迹C2的方程;
(Ⅲ)若AC、BD为椭圆C1的两条相互垂直的弦,垂足为右焦点F2,求四边形ABCD的面积的最小值.
(本小题满分12分)已知三棱锥P—ABC中,PC⊥底面ABC, ,
,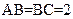 ,二面角P-AB-C为
,二面角P-AB-C为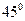 ,D、F分别为AC、PC的中点,DE⊥AP于E.
,D、F分别为AC、PC的中点,DE⊥AP于E.
(Ⅰ)求证:AP⊥平面BDE;
(Ⅱ)求平面BEF与平面BAC所成的锐二面角的余弦值.