(本小题满分12分)
在正三棱柱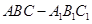 中,底面边长和侧棱都是2,D是侧棱
中,底面边长和侧棱都是2,D是侧棱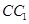 上任意一点.E是
上任意一点.E是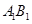 的中点.
的中点.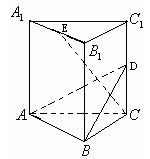
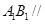 (1)求证: 平面ABD;
(1)求证: 平面ABD;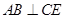 (2)求证: ;
(2)求证: ;
(3)求三棱锥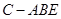 的体积。
的体积。
在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(Ⅰ)求取出的两个球上标号为相同数字的概率;
(Ⅱ)求取出的两个球上标号之积能被3整除的概率.
已知椭圆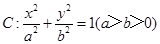 的离心率为
的离心率为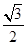 ,过右焦点
,过右焦点 且斜率为
且斜率为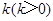 的直线与
的直线与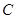 相交于
相交于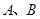 两点.若
两点.若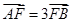 ,则
,则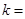
(本题满分10分)已知向量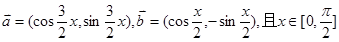 ,求
,求
(Ⅰ)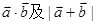 ;
;
(Ⅱ)若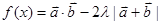 的最小值是
的最小值是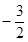 ,求实数
,求实数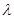 的值.
的值.
(本题满分10分)已知向量 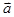 =(cos
=(cos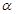 ,sin
,sin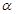 ),
),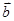 =(cos
=(cos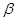 ,sin
,sin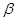 ),|
),|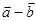 |=
|=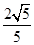 .
.
(Ⅰ)求cos(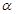 -
-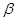 )的值;
)的值;
(Ⅱ)若0<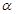 <
<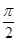 ,-
,-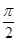 <
<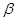 <0,且sin
<0,且sin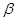 =-
=-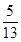 ,求sin
,求sin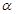 的值.
的值.
(本题满分10分) 已知函数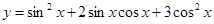 ,
,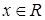 ,那么
,那么
(Ⅰ)函数的最小正周期是什么?(Ⅱ)函数在什么区间上是增函数?