如图所示,一轻弹簧左端固定在竖直墙上,右端与一物块A栓接,物块B与A接触但不粘连,开始时弹簧处于原长 状态。现用一水平力向左缓慢推B致使弹簧压缩,当物块移动S1=0.2m时撤去水平力。在弹力作用下物块AB向右运动,AB分离后,物块B继续向前滑行
状态。现用一水平力向左缓慢推B致使弹簧压缩,当物块移动S1=0.2m时撤去水平力。在弹力作用下物块AB向右运动,AB分离后,物块B继续向前滑行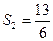 m与置于
m与置于 光滑圆弧轨道底端的物块C发生正碰并粘在一起运动,最后两物块恰好能滑到
光滑圆弧轨道底端的物块C发生正碰并粘在一起运动,最后两物块恰好能滑到 圆弧轨道的最高点:已知三物块与水平面的动摩擦因数均为0.3,圆弧轨道半径R=0.2m,物块。A、B的质量相同m1=m2=0.2kg,物块C的质量m3=0.4kg,三物块均可视为质点,取g=10m/s2,求:
圆弧轨道的最高点:已知三物块与水平面的动摩擦因数均为0.3,圆弧轨道半径R=0.2m,物块。A、B的质量相同m1=m2=0.2kg,物块C的质量m3=0.4kg,三物块均可视为质点,取g=10m/s2,求:
(1)B、C两个物块第一次返回到圆弧底端时圆弧轨道对两物块的支持力:
(2)A、B两个物块分离时的速度;
(3)水平力F对物块B做的功。
“勇气”号火星车在火星表面登陆的时机选择在6万年来火星距地球最近的一次,火星与地球之间的距离仅有5580万千米,如图所示,设火星车在登陆前绕火星做匀速圆周运动,距火星表面高度为H,火星半径为R,绕行N圈的时间为t,求:
(1)若地球、火星绕太阳公转为匀速圆周运动,其周期分别为T地 T火,比较它们的大小.
(2)火星的平均密度(用R、H、N、t及万有引力常数G表示).
(3) 火星车登陆后不断地向地球发送所拍摄的照片,地球上接收到的第一张照片大约是火星车多少秒前拍摄的?
火星车登陆后不断地向地球发送所拍摄的照片,地球上接收到的第一张照片大约是火星车多少秒前拍摄的?
(17分)如图所示,传递带可以把质量m=20kg的行李包沿水平方向送上小车左端,小车的质量M=80kg,原来静止停在光滑水平道上,行李包与车间的动摩擦因数μ=0.5,小车长1.5m,如果传送带以v=5.0m/s的水平速度将行李包送上小车,求行李包在小车上滑行的时间多少?(g取10m/s )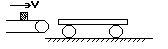
 如图所示,A、B、C三个物体质量均为m,其中厚度相同的A、B位于光滑的水平面上,可视为质点的小物块C放在静止的B物体上,物体A以速度v0向物体B运动,与B发生碰撞(碰撞时间极短),碰后A、B以相同的速度运动,但互不粘连;C滑过B后又在A上滑行,最后停在A上,与A一起以
如图所示,A、B、C三个物体质量均为m,其中厚度相同的A、B位于光滑的水平面上,可视为质点的小物块C放在静止的B物体上,物体A以速度v0向物体B运动,与B发生碰撞(碰撞时间极短),碰后A、B以相同的速度运动,但互不粘连;C滑过B后又在A上滑行,最后停在A上,与A一起以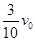 的速度运动。求:
的速度运动。求:
(1)物体B最终的速度;
(2)小物块C在物体A和物体B上滑行过程中由于摩擦产生的热量之比。
质量为m=1kg的小物块轻轻放在水平匀速运动的传送带上的P点,随传送带运动到A点后水平抛出,小物块恰好无碰撞的沿圆弧切线从B点进入竖直光滑圆孤轨道下滑。B、C为圆弧的两端点,其连线水平.已知圆弧半径R=1.0m,轨道最低点为E。A点距水平面的高度h=0.8m,距B点的水平距离x=1.2m。小物块离开C点恰能无碰撞的沿固定斜面向上运动,0.8s后经过D点,物块与斜面间的滑动摩擦因数为μ=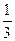 (g=10m/s2,sin300="0.5" sin37°=0.6,sin450=0.71)试求:
(g=10m/s2,sin300="0.5" sin37°=0.6,sin450=0.71)试求: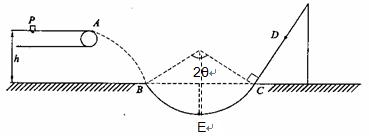
小物块离开A点的水平初速度v1
小物块经过O点时对轨道的压力
斜面上CD间的距离
如图所示,在光滑桌面上放着木板A,长度为L=1.0m,在木板A的左上端放一可视为质点的小金属块,它的质量和木板的质量相等,最初它们是静止的。现让小金属块以V0 =2.0m/s的初速度开始向右滑动,当滑动到木板A的右端时,滑块的速度为V1="1m/s," 取 g= l0m/s2,求: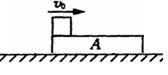
小金属块刚滑过木板A时的速度及滑块与木板间的摩擦因数;
木板A的位移。