(本小题满分12分)
已知数列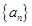 的首项为2,点
的首项为2,点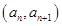 在函数
在函数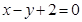 的图像上
的图像上
(Ⅰ)求数列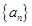 的通项公式;
的通项公式;
(Ⅱ)设数列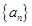 的前
的前 项之和为
项之和为 ,求
,求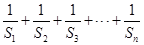 的值.
的值.
(本题14分)
设函数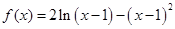 .
.
(1)求函数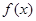 的单调递增区间;
的单调递增区间;
(2)若关于 的方程
的方程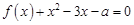 在区间
在区间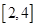 内恰有两个相异的实根,求实数
内恰有两个相异的实根,求实数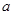 的取值范围.
的取值范围.
(本题12分)
已知函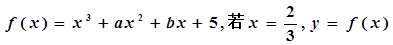 有极值,且曲线
有极值,且曲线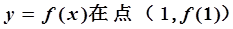 处的切线斜率为3.
处的切线斜率为3.
(1)求函数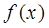 的解析式;
的解析式;
(2)求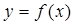 在[-4,1]上的最大值和最小值。
在[-4,1]上的最大值和最小值。
(3)函数 有三个零点,求实数
有三个零点,求实数 的取值范围.
的取值范围.
(本题12分)
在 中,角
中,角 所对的边为
所对的边为 已知
已知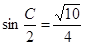 .
.
(1)求 的值;
的值;
(2)若 的面积为
的面积为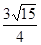 ,且
,且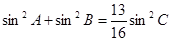 ,求
,求 的值.
的值.
(本题12分)某公司是专门生产健身产品的企业,第一批产品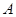 上市销售40天内全部售完,该公司对第一批产品
上市销售40天内全部售完,该公司对第一批产品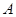 上市后的市场销售进行调研,结果如图(1)、(2)所示.其中(1)的抛物线表示的是市场的日销售量与上市时间的关系;(2)的折线表示的是每件产品
上市后的市场销售进行调研,结果如图(1)、(2)所示.其中(1)的抛物线表示的是市场的日销售量与上市时间的关系;(2)的折线表示的是每件产品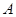 的销售利润与上市时间的关系.
的销售利润与上市时间的关系.
(1)写出市场的日销售量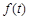 与第一批产品A上市时间t的关系式;
与第一批产品A上市时间t的关系式;
(2)第一批产品A上市后的第几天,这家公司日销售利润最大,最大利润是多少?