本题共有2个小题，第1小题满分8分，第2小题满分4分.
在正四棱柱
中，已知底面
的边长为2，点P是
的中点，直线AP与平面
成
角.
（文）（1）求
的长；
（2）求异面直线
和AP所成角的大小.(结果用反三角函数值表示)；
（理）（1）求异面直线和AP所成角的大小.(结果用反三角函数值表示) ；
（2）求点
到平面
的距离.
为了让学生了解更多“奥运会”知识，某中学举行了一次“奥运知识竞赛”，共有800名学生参加了这次竞赛，为了解本次竞赛成绩情况，从中抽取部分学生的成绩(得分均为整数，满分为100分)进行统计．请你根据尚未完成并有局部污损的频率分布表，解答下列问题：
| 分组 |
频数 |
频率 |
| 60.5～70.5 |
0.16 |
|
| 70.5～80.5 |
10 |
|
| 80.5～90.5 |
18 |
0.36 |
| 90.5～100.5 |
||
| 合计 |
50 |
(1)若用系统抽样的方法抽取50个样本，现将所有学生随机地编号为000,001,002，…，799，试写出第二组第一位学生的编号；
(2)填充频率分布表的空格(将答案直接填在表格内)，并作出频率分布直方图；
(3)若成绩在85.5～95.5分的学生为二等奖，问参赛学生中获得二等奖的学生约为多少人？
．选修4－5：不等式选讲
已知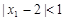
，
．
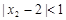（1）求证：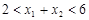
，
；
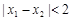（2）若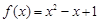
，求证：
．
选修4－4：坐标系与参数方程
已知直线
的参数方程是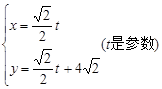
，圆C的极坐标方程为
．
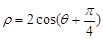（1）求圆心C的直角坐标；
（2）由直线上的点向圆C引切线，求切线长的最小值．
选修4—1：几何证明选讲
如图，AB、CD是圆的两条平行弦，BE//AC，BE交CD于E、交圆于F，过A点的切线交DC的延长线于P，PC=ED=1，PA=2．
（1）求AC的长；
（2）求证：BE＝EF．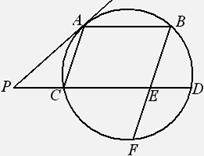
（本小题满分12分）
已知函数f（x）是定义在[-e,0）∪（0,e]上的奇函数，当x∈（0,e],f（x）=ax+lnx（其中e是自然对数的底数，a∈R）
（1）求f（x）的解析式；
（2）设g（x）=
,x∈[-e,0）,求证：当a=-1时，f（x）>g（x）+
;
（3）是否存在实数a，使得当x∈[-e,0）时f（x）的最小值是3 如果存在，求出实数a的值；如果不存在，请说明理由．