(本题12分)
如图:△ABC的角平分线AD的延长线交它的外接圆于点E。
①证明:AB ·AC=AD·AE;
·AC=AD·AE;
②若△ABC的面积S=  AD·AE,求∠BAC的大小。
AD·AE,求∠BAC的大小。
设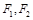 分别是椭圆
分别是椭圆 的左、右焦点.
的左、右焦点.
⑴若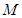 是该椭圆上的一点,且
是该椭圆上的一点,且 ,求
,求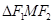 的面积;
的面积;
⑵若 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求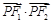 的最大值和最小值;
的最大值和最小值;
⑶设过定点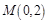 的直线
的直线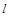 与椭圆交于不同的两点
与椭圆交于不同的两点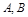 ,且
,且 为锐角(其中
为锐角(其中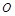 为坐标原点),求直线
为坐标原点),求直线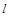 的斜率
的斜率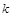 的取值范围.
的取值范围.
已知点 ,
,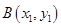 ,
,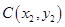 在抛物线
在抛物线 (
( )上,
)上, 的重心与此抛物线的焦点
的重心与此抛物线的焦点 重合(如图)
重合(如图)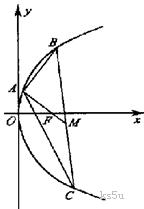
⑴写出该抛物线的方程和焦点 的坐标;
的坐标;
⑵求线段 中点
中点 的坐标;
的坐标;
⑶求 所在直线的方程.
所在直线的方程.
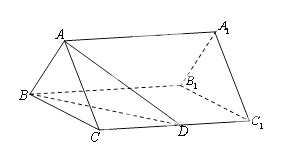
如图,已知正三棱柱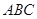 —
—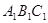 的底面边长是
的底面边长是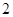 ,
,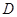 是侧棱
是侧棱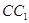 的中点,直线
的中点,直线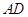 与侧面
与侧面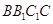 所成的角为
所成的角为 .
.
⑴求此正三棱柱的侧棱长;
⑵求二面角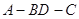 的平面角的正切值;
的平面角的正切值;
⑶求直线 与平面
与平面 的所成角的正弦值.
的所成角的正弦值.
已知圆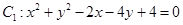 与直线
与直线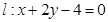 相交于
相交于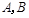 两点.
两点.
⑴求弦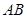 的长;
的长;
⑵若圆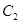 经过
经过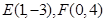 ,且圆
,且圆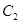 与圆
与圆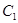 的公共弦平行于直线
的公共弦平行于直线 ,求圆
,求圆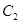 的方程.
的方程.
已知函数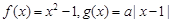 .
.
(1)若关于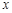 的方程
的方程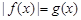 只有一个实数解,求实数
只有一个实数解,求实数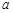 的取值范围;
的取值范围;
(2)若当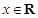 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数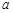 的取值范围;
的取值范围;
(3)探究函数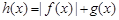 在区间
在区间 上的最大值(直接写出结果,不需给出演算步骤).
上的最大值(直接写出结果,不需给出演算步骤).