.(本小题满分14分)
如图,已知正方体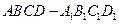 的棱长为2,E、F分别是
的棱长为2,E、F分别是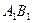 、
、 的中点,过
的中点,过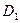 、E、F作平面
、E、F作平面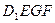 交
交 于G..
于G..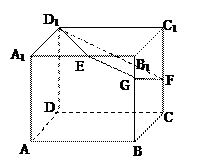
(Ⅰ)求证: ∥
∥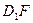 ;
;
(Ⅱ)求二面角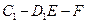 的余弦值;
的余弦值;
(Ⅲ)求正方体被平面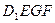
 所截得的几何体
所截得的几何体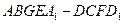 的体积.
的体积.
【2015高考湖南,理17】设 的内角
的内角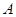 ,
,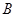 ,
,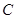 的对边分别为
的对边分别为 ,
, ,
,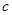 ,
,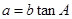 ,且
,且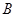 为钝角.
为钝角.
(1)证明: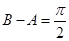 ;
;
(2)求 的取值范围.
的取值范围.
【2015高考广东,理16】在平面直角坐标系 中,已知向量
中,已知向量 ,
,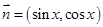 ,
, .
.
(1)若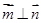 ,求tan x的值;
,求tan x的值;
(2)若 与
与 的夹角为
的夹角为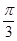 ,求
,求 的值.
的值.
【2015高考北京,理15】已知函数 .
.
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)求 在区间
在区间 上的最小值.
上的最小值.
【2015高考陕西,理17】(本小题满分12分)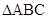 的内角
的内角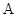 ,
,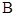 ,
,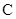 所对的边分别为
所对的边分别为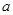 ,
,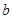 ,
,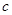 .向量
.向量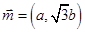 与
与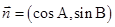 平行.
平行.
(Ⅰ)求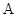 ;
;
(Ⅱ)若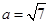 ,
,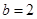 求
求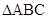 的面积.
的面积.
【2015高考湖北,理17】某同学用“五点法”画函数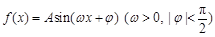 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
 |
0 |
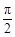 |
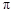 |
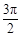 |
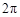 |
 |
 |
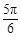 |
|||
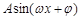 |
0 |
5 |
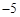 |
0 |
(Ⅰ)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数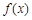 的解析式;
的解析式;
(Ⅱ)将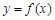 图象上所有点向左平行移动
图象上所有点向左平行移动
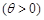 个单位长度,得到
个单位长度,得到 的图象.若
的图象.若 图象的一个对称中心为
图象的一个对称中心为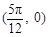 ,求
,求 的最小值.
的最小值.