(本小题满分12分)
设函数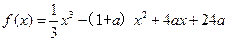 ,其中常数a>1.
,其中常数a>1.
(Ⅰ)讨论f (x)的单调性;
(Ⅱ)若当x≥0时,f (x)>0恒成立,求a的取值范围.
某小组6个人排队照相留念。(1)若分成两排照相,前排2人,后排4人,有多少种不同的排法?(2)若分成两排照相,前排2人,后排4人,但其中甲必须在前排,乙必须在后排,有多少种排法?(3)若排成一排照相,甲、乙两人必须在一起,有多少种不同的排法?(4)若排成一排照相,其中甲必在乙的右边,有多少种不同的排法?(5)若排成一排照相,其中有3名男生3名女生,且男生不能相邻有多少种排法?(6)若排成一排照相,且甲不站排头乙不站排尾,有多少种不同的排法?
设函数
(1)若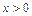 证明:
证明: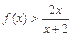 。
。
(2)若不等式 对于
对于 及
及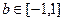 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
已知正数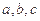 满足
满足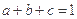 证明
证明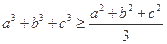
若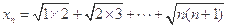 (n为正整数),
(n为正整数),
求证:不等式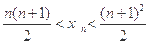 对一切正整数n恒成立
对一切正整数n恒成立
设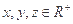 ,求证:
,求证: