(本小题满分12分)已知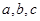 分别为
分别为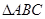 三个内角
三个内角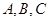 的对边,
的对边,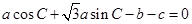 。
。
(1)求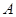 的大小;
的大小;
(2)若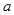 = 7,求
= 7,求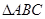 的周长的取值范围.
的周长的取值范围.
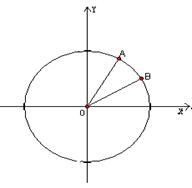
(本小题满分12分)如图,在平面直角坐标系xoy中,以O为顶点,x轴正半轴为始边作两个锐角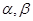 ,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为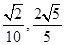 。
。
(1)求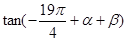 的值;
的值;
(2)求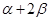 的值.
的值.
(本小题满分10分) 已知向量 ,
,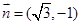 ,且
,且 ,A为锐角.
,A为锐角.
(1)求角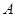 的大小;
的大小;
(2)求函数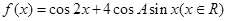 的值域.
的值域.
(本小题满分12分)已知函数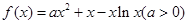 .
.
(1)若函数满足 ,且在定义域内
,且在定义域内 恒成立,求实数b的取值范围;
恒成立,求实数b的取值范围;
(2)若函数 在定义域上是单调函数,求实数a的取值范围;
在定义域上是单调函数,求实数a的取值范围;
(3)当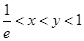 时,试比较
时,试比较 与
与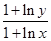 的大小.
的大小.
(本小题满分12分)已知函数 图象上点
图象上点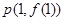 处的切线方程为2x-y-3=0.
处的切线方程为2x-y-3=0.
(1)求函数 的解析式及单调区间;
的解析式及单调区间;
(2)若函数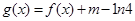 在
在 上恰有两个零点,求实数m的取值范围.
上恰有两个零点,求实数m的取值范围.