如图,三棱柱ABC-A1B1C1的侧棱AA1⊥平面ABC,△ABC为正三角形,且侧面AA1C1C是边长为2的正方形,E是 的中点,F在棱CC1上。
的中点,F在棱CC1上。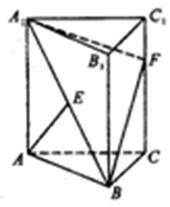
(1)当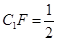 CF时,求多面体ABCFA1的体积;
CF时,求多面体ABCFA1的体积;
(2)当点F使得A1F+BF最小时,判断直线AE与A1F是否垂直,并证明的结论。
火车站 北偏东
北偏东 方向的
方向的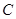 处有一电视塔,火车站正东方向的
处有一电视塔,火车站正东方向的 处有一小汽车,测得
处有一小汽车,测得 距离为31
距离为31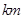 ,该小汽车从
,该小汽车从 处以60公里每小时的速度前往火车站,20分钟后到达
处以60公里每小时的速度前往火车站,20分钟后到达 处,测得离电视塔21
处,测得离电视塔21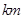 ,问小汽车到火车站还需多长时间?
,问小汽车到火车站还需多长时间?
已知数列{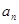 }中,
}中, 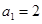 ,
,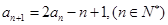 ,
,
(1)求证数列{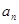
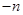 }为等比数列.
}为等比数列.
(2)判断265是否是数列{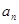 }中的项,若是,指出是第几项,并求出该项以前所有项的和(不含265),若不是,说明理由.
}中的项,若是,指出是第几项,并求出该项以前所有项的和(不含265),若不是,说明理由.
已知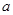 ,
, ,
,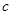 分别为
分别为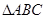 三个内角
三个内角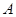 ,
,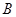 ,
,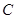 的对边,
的对边, 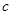 =
=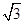
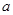 sin
sin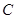
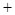
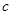 cos
cos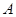 .
.
(1)求角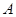 ;
;
(2)若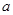 =
=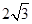 ,
,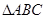 的面积为
的面积为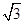 ,求
,求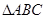 的周长.
的周长.
已知函数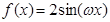 ,其中常数
,其中常数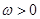 .
.
(1)令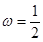 ,求函数
,求函数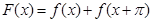 的单调区间;
的单调区间;
(2)令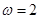 ,将函数
,将函数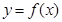 的图像向左平移
的图像向左平移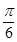 个单位,再往上平移
个单位,再往上平移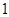 个单位,得到函数
个单位,得到函数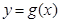 的图像.对任意的
的图像.对任意的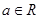 ,求
,求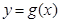 在区间
在区间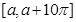 上零点个数的所有可能值.
上零点个数的所有可能值.
已知点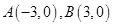 ,动点P 满足:|PA|=2|PB|.
,动点P 满足:|PA|=2|PB|.
(1)若点P的轨迹为曲线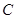 ,求此曲线的方程;
,求此曲线的方程;
(2)若点Q在直线l1: x+y+3=0上,直线l2经过点Q且与曲线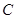 只有一个公共点M,求|QM|的最小值.
只有一个公共点M,求|QM|的最小值.