如图,三棱锥SABC中,SC丄底面ABC, ,
, ,M
,M 为SB中点,N在AB上,满足
为SB中点,N在AB上,满足

(I)求点N到平面SBC的距离;
(II)求二面角C-MN-B的大小.
近期世界各国军事演习频繁,某国一次军事演习中,空军同时出动了甲、乙、丙三架不同型号的战斗机对一目标进行轰炸,已知甲击中目标的概率是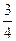 ;甲、丙同时轰炸一次,目标未被击中的概率是
;甲、丙同时轰炸一次,目标未被击中的概率是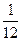 ;乙、丙同时轰炸一次都击中目标的概率是
;乙、丙同时轰炸一次都击中目标的概率是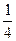 。
。
(Ⅰ)求乙、丙各自击中目标的概率。
(Ⅱ)求目标被击中的概率。
12分)
如图所示,四棱锥P—ABCD的底面ABCD是正方形,PD 底面ABCD,PD=AD
底面ABCD,PD=AD
(Ⅰ)求证:平面PAC 平面PBD
平面PBD
(Ⅱ)求PC与平面PBD所成角
数列 中,a1=2,an+1=an+cn(c是常数,n=1,2,3……)且a1,a2,a3成公比不为1的等比数列
中,a1=2,an+1=an+cn(c是常数,n=1,2,3……)且a1,a2,a3成公比不为1的等比数列
(Ⅰ)求c的值
(Ⅱ)求 的通项公式
的通项公式
设△ABC的内角A、B、C的对边分别为a、b、c,已知b2+c2=a2+ bc,求:
bc,求:
(Ⅰ)A的大小
(Ⅱ)2sinBcosc-sin(B-C)的值
已知抛物线方程 ,过点
,过点 作抛物线的两条切线
作抛物线的两条切线 ,切点分别为
,切点分别为 .
.
(Ⅰ)求证直线 过定点
过定点 ;
;
(Ⅱ)求△ (
( 为坐标原点)面积的最小值.
为坐标原点)面积的最小值.