设函数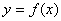 是定义在
是定义在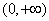 上的减函数,并且满足
上的减函数,并且满足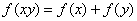 ,
,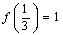
(1)求 ,
,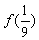 ,
,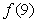 的值,(2)如果
的值,(2)如果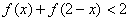 ,求x的取值范围。
,求x的取值范围。
(本小题满分12分)
已知射手甲射击一次,击中目标的概率是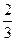 .
.
(1)求甲射击5次,恰有3次击中目标的概率;
(2)假设甲连续2次未击中目标,则停止其射击,求甲恰好射击5次后,被停止射击的概率.
(本小题满分12分)
在△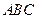 中,角
中,角 所对的边分别为
所对的边分别为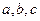 ,已知
,已知 ,
,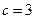 ,
,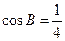 .
.
(1)求 的值;(2)求
的值;(2)求 的值.
的值.
设数列 满足
满足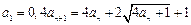 ,令
,令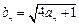 .
.
⑴试判断数列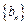 是否为等差数列?并说明理由;
是否为等差数列?并说明理由;
⑵若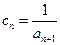 ,求
,求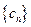 前
前 项的和
项的和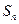 ;
;
⑶是否存在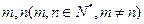 使得
使得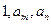 三数成等比数列?
三数成等比数列?
如图,有一壁画,最高点A处离地面4m,最低点B处离地面2m,若从离地高1.5m的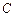 处观赏它,则离墙多远时,视角
处观赏它,则离墙多远时,视角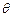 最大?
最大?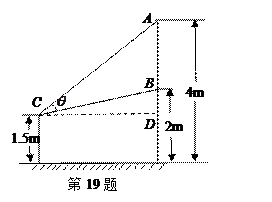
已知函数 ,
,
(1) 若不等式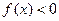 的解集是
的解集是 ,求
,求 的值;
的值;
(2)若 ,
, ,求函数
,求函数 的最大值;
的最大值;
(3) 若对任意x∈ ,不等式
,不等式 >0恒成立,求实数
>0恒成立,求实数 的取值范围。
的取值范围。