已知奇函数, 的
的 图象在x=2处的切线方程为
图象在x=2处的切线方程为
(I )求 的解析式;
的解析式;
(II)是否存 在实数,m,n使得函数
在实数,m,n使得函数 在区间
在区间 上的最小值为m,最大值为n.若存在,求出这样一组实数m,n,若不存在,则说明理由.
上的最小值为m,最大值为n.若存在,求出这样一组实数m,n,若不存在,则说明理由.
若sin( -α)=-
-α)=-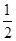 ,sin(
,sin( +β)=
+β)=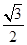 ,其中
,其中 <α<
<α< ,
, <β<
<β< ,求 角(α+β)的值.
,求 角(α+β)的值.
已知角α终边上一点P(-4,3),求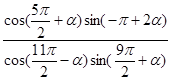 的值.
的值.
(本小题满分14分)已知集合 是满足下列性质的函数
是满足下列性质的函数 的全体:在定义域内存在
的全体:在定义域内存在 ,使得
,使得 成立。
成立。
(Ⅰ)函数 是否属于集合
是否属于集合 ?说明理由;
?说明理由;
(Ⅱ)设函数 ,求
,求 的取值范围;
的取值范围;
(Ⅲ)设函数 图象与函数
图象与函数 的图象有交点,
的图象有交点,
证明:函数 。
。
(本小题满分13分)已知函数
 .
.
(1)求函数 的最小正周期和最大值;
的最小正周期和最大值;
(2)在给出的直角坐标系中,画出函数 在区间
在区间 上的图象.
上的图象.
(3)设0<x< ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围.
(本小题满分12分)如图所示, 中,
中, ,
, ,
, ,
,
(1)试用向量 ,
, 来表示
来表示 .
.
(2)AM交DN于O点,求AO:OM的值.