设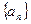
为递增等差数列，Sn为其前n项和，满足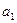
-
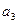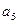=S10，S11=33。
（1）求数列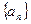的通项公式
及前n项和Sn；
（2）试求所有的正整数m，使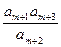
为正整数。
（本小题满分10分）
在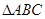
中内角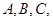
的对边分别为
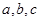，且
（1）求
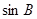的值；
（2）如果b=4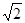
，且a=c,求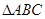的面积.
如图所示，已知P(4，0)是圆x2+y2=36内的一点，A、B是圆上两动点，且满足∠APB=90°，求矩形APBQ的顶点Q的轨迹方程.
自点A(-3，3)发出的光线L射到x轴上，被x轴反射，其反射光线所在直线与圆x2+y2-4x-4y+7＝0相切，求光线L所在的直线方程.
直线l经过P（2,3）,且在x,y轴上的截距相等,试求该直线方程.
已知正方形ABCD 对角线AC所在直线方程为
.抛物线
过B，D两点
（1）若正方形中心M为（2，2）时，求点N(b,c)的轨迹方程。
（2）求证方程
的两实根
，
满足