已知空间三点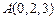 ,
,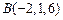 ,
,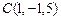
(1)求以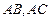 为边的平行四边形的面积;
为边的平行四边形的面积;
(2)若向量a分别与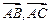 垂直,且|a|=
垂直,且|a|=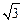 ,求a的坐标.
,求a的坐标.
已知函数 在
在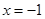 处有极大值
处有极大值 .
.
(1)求 的解析式;
的解析式;
(2)求 的单调区间;
的单调区间;
设函数 ,
,
(1)求函数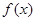 的单调区间;
的单调区间;
(2)若当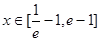 时,不等式
时,不等式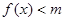 恒成立,求实数
恒成立,求实数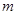 的取值范围;
的取值范围;
(3)若关于 的方程
的方程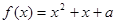 在区间
在区间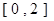 上恰好有两个相异的实根,求实数
上恰好有两个相异的实根,求实数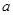 的取值范围.
的取值范围.
如图,已知焦点在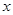 轴上的椭圆
轴上的椭圆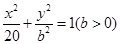 经过点
经过点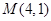 ,直线
,直线
交椭圆于 不同的两点.
不同的两点.
(1)求该椭圆的标准方程;
(2)求实数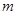 的取值范围;
的取值范围;
(3)是否存在实数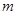 ,使△
,使△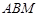 是以
是以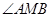 为直角的直角三角形,若存在,求出
为直角的直角三角形,若存在,求出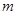 的值,若不存,请说明理由.
的值,若不存,请说明理由.
某商品每件成本9元,售价为30元,每星期卖出144件. 如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值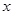 (单位:元,
(单位:元, )的平方成正比.
)的平方成正比.
已知商品单价降低2元时,一星期多卖出8件.
(1)将一个星期的商品销售利润表示成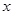 的函数;
的函数;
(2)如何定价才能使一个星期的商品销售利润最大?
如图,三棱柱 的底面是边长为2的正三角形,且侧棱垂直于底面,侧棱长是,D是AC的中点。
的底面是边长为2的正三角形,且侧棱垂直于底面,侧棱长是,D是AC的中点。
(1)求证: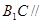 平面
平面 ;
;
(2)求二面角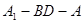 的大小;
的大小;
(3)求直线 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.