如图所示,已知在直角梯形 中,
中,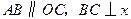 轴于点
轴于点 .动点
.动点 从
从 点出发,沿
点出发,沿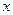 轴正方向以每秒1个单位长度的速度移动.过
轴正方向以每秒1个单位长度的速度移动.过 点作
点作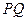 垂直于直线
垂直于直线 ,垂足为
,垂足为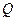 .设
.设 点移动的时间为
点移动的时间为 秒(
秒(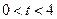 ),
),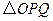 与直角梯形
与直角梯形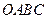 重叠部分的面积为
重叠部分的面积为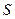 .
.
(1)求经过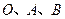 三点的抛物线解析式;
三点的抛物线解析式;
(2)求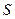 与
与 的函数关系式;
的函数关系式;
(3)将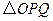 绕着点
绕着点 顺时针旋转
顺时针旋转 ,是否存在
,是否存在 ,使得
,使得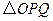 的顶点
的顶点 或
或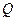 在抛物线上?若存在,直接写出
在抛物线上?若存在,直接写出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
如图,反比例函数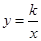 的图象与一次函
的图象与一次函 的图象交于
的图象交于 ,
,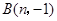 两点.
两点.求反比例函数与一次函数的解析式;
根据图象回答:当
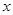 取何值时,反比例函数的值大于一次函数的值.
取何值时,反比例函数的值大于一次函数的值.
如图(1),某建筑物有一抛物线形的大门,小强想知道这道门的高度. 他先测出门的宽度 ,然后用一根长为
,然后用一根长为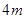 的小竹杆
的小竹杆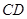 竖直地接触地面和门的内壁,并测得
竖直地接触地面和门的内壁,并测得 . 小强画出了如图(2)的草图,请你帮他算一算门的高度
. 小强画出了如图(2)的草图,请你帮他算一算门的高度 .
.

要测量一个钢板上的小孔的直径,通常采用间接的测量方法.如果用一个直径为10mm的标准钢珠放在小孔上,测的钢珠顶端与小孔平面的距离h="8" mm(如图),求此小孔的直径d.
果园有100棵桃树,一棵桃树平均结1000个桃子,现准备多种一些桃树以提高产量,试验发现,每多种一棵桃树,每棵树的产量就会减少2个,多种的桃树不能超过100棵,如果要使产量增加15.2%,那么应多种多少棵桃树?
请写出“直角三角形斜边上的中线等于斜边的一半”的逆命题,并进行证明: